|
|
|
|
Quantité
de mouvement :
Le schéma représente le système S
(supposé
pseudo isolé) constitué par un tireur, sa carabine et la balle. Lors du
tir on peut décomposer le système en deux sous-systèmes : le
sous-système A {tireur+ carabine} et
le sous-système B {la balle}. On note PA
(respectivement PB)
la quantité de mouvement de A (respectivement de B).
Données : ms= 80 kg ; mA=
80 kg ; mB =
8,0 g ; VB= 3000 km.h-1 ;
24*36=8,7 102 ; 24/36 =0,67 ; 36/24 = 1,5.
a) Le vecteur quantité de mouvement de S se conserve. Vrai.
b) Après le tir, on a :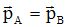 . Faux. . Faux.
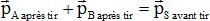
c) La valeur de PB,après le tir, est de 87 kg.m.s-1.
Faux.
pB = 8,0 10-3
*3000 / 3,6 =24 / 3,6 = 6,7 kg m s-1.
d) Le tireur est repoussé vers l'arrière avec une vitesse de 0,3 km.h-1.
Vrai.
-mA vA
+mB vB = mS* vitesse initiale de S = 0.
vA
=mB vB / mA =8,0 10-3
/ 80 *3000 =8,0*3 / 80 = 0,3 km /h.
|
.
|
Sport de contact.
Il y a plaquage lorsqu'un joueur porteur du ballon, sur ses pieds dans
le champ de jeu, est simultanément tenu par un ou plusieurs
adversaires, qu'il est mis au sol et/ou que le ballon touche le sol. Ce
joueur est appelé joueur plaqué. D'après http://www.francerugby.fr.
Un joueur A de masse mA = 115 kg est animé d'une vitesse vA =5,0 m/s est plaqué par un joueur B de masse mB = 110 kg de vitesse négligeable.
Dans quel référentiel les vitesses sont-elles définies ?
Les vitesses sont définies dans le référentiel terrestre supposé galiléen.
On suppose que l'ensemble des deux joueurs est un système isolé.
Exprimer, en justifiant, la vitesse des deux joueurs liés après l'impact puis calculer sa valeur.
Ecrire la conservation du vecteur quantité de mouvement du système isolé constitué par les deux joueurs.
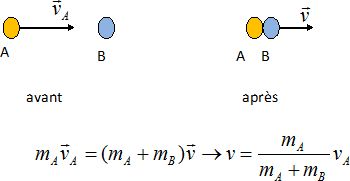
v = 115 / (115+110) *5,0 =2,555 ~2,6 m/s.
.
|
|
Fusée au décollage.
On se propose dans cette partie d'étudier le décollage de la fusée.
Dans le référentiel terrestre supposé galiléen, à l'instant t=0, la
fusée est immobile. A la ate t= 1 s, la fusée a éjecté une masse de gaz
mg à la vitesse vg. Sa masse est alors notée mf et sa vitesse vf.
On donne g = 9,78 m s-2 ; débit d'élection des gaz au décollage D = 2,9 103 kg s-1; vg = 4,0 km/s. Masse de la fusée au décollage : 7,8 102 tonnes.
Dans un modèle simplifié, on suppose que le système {fusée + gaz} est isolé.
Donner l'expression vectorielle de la vitesse de la fusée.
A
t=0, le système étant immobile, sa quantité de mouvement est nulle. Le
système étant isolé, le vecteur quantité de mouvement du système se
conserve.
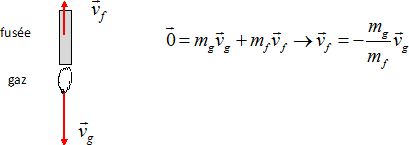
La fusée est propulsée par réaction.
|
|