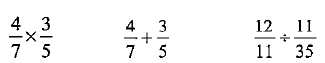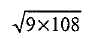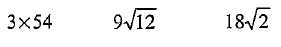|
La fraction suivante est le résultat de l'opération :
B = 12/35 = 3*2*2 / ( 7*5) = 4 / 7 x 3 / 5.
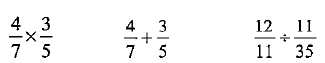 Un groupe d'élèves comprend 60 % de garçons. 40%
de ces garçons étudient l'allemand, les autres l'espagnol et 60 % des
filles étudient l'allemand, les autres l'anglais.On choisit au hasard
un élève du groupe. Quelle est la probabilité d'avoir choisi une fille
qui étudie l'allemand ?
Soit N le nombre d'élèves : 0,6 N garçons et 0,4 N filles.
0,6 *0,4 N = 0,24 N garçons + 0,4 *0,6 N = 0,24 N filles soit 0,48 N élèves étudient l'allemand.
Probabilité d'avoir choisi une fille étudiant l'allemand : 0,24.
Le volume d'un grain de sable est d'environ 0,014 mm3. Quel est le nombre de grains de sable contenu dans 1 m3 de sable ?
1 m3 = 109 mm3 ; 109 / 0,014 =7 1010.
L'expression 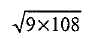 peut s'écrire : peut s'écrire : 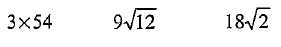
9 = 32 ; 108 = 3*32*22 ; (9*108)½ = (32 *22 *32 *3)½ =3*2*3 *3½ = 18 *3½ ou 9 *12½.
On donne l'expression littérale A = x2+3x-1. Lorsqu'on remplace x par -8, on obtient : 16-24-1 ; 64-24-1 ; -41.
(-8)2 +3(-8)-1 = 64 -24-1 =39.
Une pyramide donnée est la réduction d'une grande pyramide. Le rapport de réduction est 1/4. Le volume de la grande pyramide est de 768 m3. Calculer le volume de la petite pyramide.
Chaque dimension est divisée par 4. Un volume est le produit de trois dimensions. Le volume de la petite pyramide est : 768 / 43 = 12 m3.
Le côté d'un carré s'exprime par 2x+3 en fonction d'un nombre décimal positif x. L'aire du carré s'exprime en fonction de x par :
2(2x+3) ; (2x+3)2 ( vrai) ; 4x2+9.
Un
pack de 6 bouteilles de 1,5 L d'eau minérale contient 21600 mg de sels
minéraux dissous. La concentration ( en g/ L ) en sels minéraux est de : 2,4 ; 14,4 ; 3,6 ; 32,4.
21,6 g dans 9 L : 21,6 / 9 = 2,4 g/L.
Une imprimante a imprimé 36 pages en 1 min 48 s. Quelle est la vitesse d'impression en pages/ minute ?
36 pages imprimées en 108 s. Une page imprimée en 3 seconde ; 20 pages imprimées en 1 min.
Je diminue un prix "x"de 10 %, puis j'augmente le nouveau prix de 10 %. J'obtiens :x ; 0,90 x ; 0,99x ; 1,1x.
Après diminution de 10 % : 0,90 x.
Après augmentation de 0,90 x de 10 % : 0,9x *1,1 = 0,99 x.
Une
caisse contenant du sable pèse en tout 4,3 kg. La caisse vide pèse 1,9
kg de plus que le sable qu'elle contient. Calculer la masse de sable
contenu dans la caisse.
M : masse du sable ; M +1,9 = masse de la caisse ; M+M+1,9 = 4,3 soit M = 1,2 kg.
L'équation 2(x+5)(2x-6)=0 a pour solution : 0 ; 3 ; 2.
x+5 = 0 donne x = -2,5 ; 2x-6=0 donne x = 3.
Un
cinéma propose à ses clients un tarif d'abonnement. On achète une carte
annuelle de 30 € donnant droit à un tarif préférentiel de 4,5 € par
séance. La fonction qui le représente est :
34,5 +x ; 30 +4,5 x ( vrai) ; 34,5x ; 4,5 + 30x.
Une
échelle est appuyée contre un mur qui est perpendiculaire au sol. Les
pieds de l'échelle sont à 1,5 m du mur et le haut de cette échelle à 4
m du pied du mur. Calculer l'angle que fait l'échelle avec le sol.
tan a = 4 / 1,5 = 2,67 ; a = 69°.
Sur un cercle de diamètre AB on place un point C tel que CA = 12 cm et CB = 9 cm. Le diamètre du cercle est 15 cm ; 225 cm ; 21 cm ; incalculable.
AB2 = AC2 +BC2 = 144+81=225 ; AB = 15 cm.
Un
cylindre de hauteur h=12 cm a un rayon de base R. Une sphère a aussi un
rayon R. La sphère et le cylindre ont le même volume. R vaut :12 cm ;3 cm ; 6 cm ; 9 cm.
Volume du cylindre pR2h ; volume de la sphère :4/3 pR3. par suite : h = 4/3R et R = 3h/4 = 3*12/4 = 9 cm.
La
SNCF met en service un train rapide entre Cherbourg et Caen villes
distantes de 132 km. le train ne s'arrête pas et roule à une
vitesse moyenne de 165 km/h. Quel temps met-il pour relier les deux villes ?
1,15 h ; 50 min ; 48 min.
132/165 =0,8 hure soit 0,8*60 = 48 minutes.
En
optique, une lentille convergente placée en O donne une image renversée
CD d'un objet AB. AB = 60 cm ; OA = 2,10 m ; OC = 70 cm.
Calculer la hauteur de l'image CD.
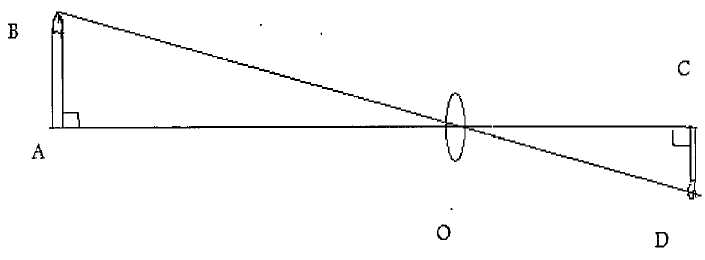 OC / OA = CD / AB ; CD = OC * AB / OA = 0,70 *0,60 / 2,10 =0,20 m = 20 cm. |