|
|
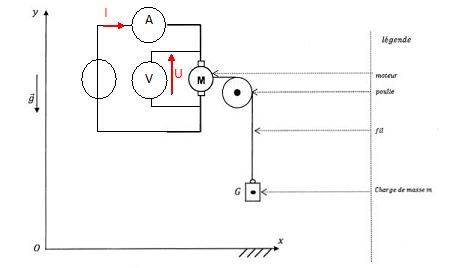
Lemonte-charge est modélisé à l'aide :
- d'un moteur à courant continu entraînant un fil pouvant être enroulé ou déroulé sur l'axe du rotor du moteur ;
- d'une poulie dans laquelle le fil s'encastre ;
- d'une masse m attachée au même fil et modélisant la charge à monter à l'aide du moteur.
Le fil est de masse négligeable, inextensible et sans raideur et la
poulie possède une liaison parfaite avec son support et est de moment
d'inertie négligeable. L'énergie mécanique délivrée par le moteur est
ainsi intégralement transférée à la charge de masse m.
On note : We : le transfert d'énergie reçu par le moteur via son alimentation ;
Wm : quantité d'énergie délivrée par le moteur sous forme mécanique ;
Wu : énergie mise en jeu pour lever la charge.
L'alimentation électrique du moteur sert également à compenser des pertes par effet Joule, notée WJ, et des pertes énergétiques liées aux frottements essentiellement solides du rotor sur son axe, notées Wf. Aucun frottement de type fluide n'est à prendre en compte.
Les grandeurs We, Wm, WJ, Wu et Wf sont comptées positivement.
Pourquoi
parle-t-on de pertes ? Ces pertes énergétiques sont-elles à priori en
contradiction avec le principe de conservation de l'énergie ? Justifier.
On appelle "perte" l'énergie qui n'est pas utilisée pour monter la
charge. Il s'agit d'une conversion d'une partie de l'énergie électrique
reçue par le moteur en énergie thermique et non pas d'énergie perdue.
L'énergie totale du système ( le monte-charge et moteur ) se conserve.
Donner une relation entre We, Wm, Wj, Wf.
We = Wm + Wj + Wf.
On note h le rendement global de la chaîne énergétique.
Définir succinctement la notion de rendement. Donner l'expression et l'unité du rendement.
Le
rendement est le rapport entre l'énergie utile pour monter la charge à
l'énergie dépensée. S'agissant du rapport de deux énergies, le
rendement est sans unité.
h = Wu/We.
On va chercher à exprimer Wu. On suppose le champ de pesanteur terrestre g uniforme dans le référentiel du laboratoire supposé galiléen.
Donner l'expression de l'énergie potentielle, notée Ep de la masse m lorsque son centre de gravité G est à l'altitude y.On prendra l'origine de l'énergie potentielle en y=0.
Ep = mgy.
La masse m est montée d'une hauteur H depuis le sol. Les vitesses initiale et finale sont nulles dans cette expérience.
Donner
l'expression de Wu en fonction de m, g et H.
La variation de l'énergie cinétique de la masse m est nulle ; l'énergie mécanique du système est constante ; Wu est égale à la variation de l'énergie potentielle : Wu = mg H.
On souhaite connaître la valeur de We par mesure
expérimentale. On suppose le régime transitoire, lié à la mise en route
du moteur, suffisamment court par rapport à la durée Dt de l'expérience, pour considérer que le régime stationnaire soit directement établi ( vitesse du moteur constante ).
Compléter le schéma en y faisant apparaître une alimentation continue, un ampèremètre et un voltmètre.
Voir schéma ci-dessus.
Donner l'expression de We.
We = UI Dt.
On mesure H=0,81 m, U = 9,0 V, I = 0,10 A et Dt = 5,0 s pour une masse m = 500 g.
Donner la valeur du rendement.
h = mgH / (UIDt) = 0,50*9,8*0,81 / (9,0*0,10*5,0) =0,88.
Les pertes par effet Joule sont liées à la résistance R du moteur. On donne R = 10 ohms
Exprimer puis calculer Wj.
Wj = RI2Dt = 10*0,12*5,0 =0,50 J
En déduire Wf. Quelle est la principale source des pertes d'énergie ?
Wf = We-Wu-Wj = 9,0*0,10*5,0-0,5*9,8*0,81 -0,5 =4,5-3,97-0,5 =0,031 J.
Les pertes par effet Joule sont bien plus importantes que les pertes par frottement solide.
|
.
|
Etude cinématique de la montée de la charge.
Le
professeur traite l'enregistrement chronophotographique d'une vidéo
réalisée en salle de classe pour mener l'étude cinématique de la montée
de la charge.
Le système étudié est la charge, solide indéformable. Les
positions successives d'un point du système sont marquées sur l'écran.
Pour chacune d'elles, le logiciel utilisé indique dans le tableau
associé, la date ( colonne 1 ), ses coordonnées dans un repère
orthonormé défini par l'utilisateur et la vitesse instantanée du
système dans le référentiel du laboratoire. Le dispositif permet de réaliser une capture d'écran tous les 2/15 s.
| t(s) |
x(m) | y(m)
|
v(m/s)
|
| 0,133 |
0 | 0,0417
|
0,2704
|
| 0,267 | 0
|
0,0725
|
0,2799
|
0,400
|
0
|
0,114
|
0,2894
|
0,533
|
0
|
0,158
|
0,3038
|
0,667
|
0
|
0,192
|
0,3056
|
0,800
|
0
|
0,236
|
0,3034
|
0,934
|
0
|
0,279
|
0,3113
|
1,067
|
0
|
0,317
|
0,3089
|
1,200
|
0
|
0,359
|
0,3113
|
1,334
|
0
|
0,4020
|
0,3143
|
1,467
|
0
|
0,444
|
0,3103
|
1,600
|
0
|
0,484
|
0,3009
|
1,734
|
0
|
0,525
|
0,2996
|
1,867
|
0
|
0,562
|
0,3071
|
2,000
|
0
|
0,605
|
0,3129
|
2,134
|
0
|
0,649
|
0,2991
|
2,267
|
0
|
0,690
|
0,2661
|
2,401
|
0
|
0,719
|
0,2328
|
On évalue l'incertitude sur la vitesse à 0,01 m/s.
Donner la nature de ce mouvement ( lignes 4 à 14 ).
Le
mouvement est rectiligne vertical. La valeur de la vitesse est
pratiquement constante ( 0,31 m/s ) : le mouvement est uniforme.
Etablir l'équation horaire y(t) de ce mouvement sachant que y(t=0) = y0.
La position est une primitive de la vitesse y = vt +y0 = 0,31 t + y0.
Représenter
l'allure des graphes y(x), y(t), v(t), v(y). Quelles sont les
interprétations à attendre des élèves pour chaque graphe.
Comment ce dispositif permet-il de déterminer la fréquence de rotation de la poulie de rayon Rp = 2 cm ?
Vitesse angulaire ( en rad/s) de la poulie w = v/Rp.
Fréquence de rotation ( tour / s ou hertz ) de la poulie : f = w/(2p).
Afin d'évaluer l'acquisition par ses élèves, le professeur à le choix entre les deux exercices suivants.
Exercice 1 :
Le graphe ci-dessous représente la distance d parcourue par un artisan depuis son entreprise au cours d'un déplacement.
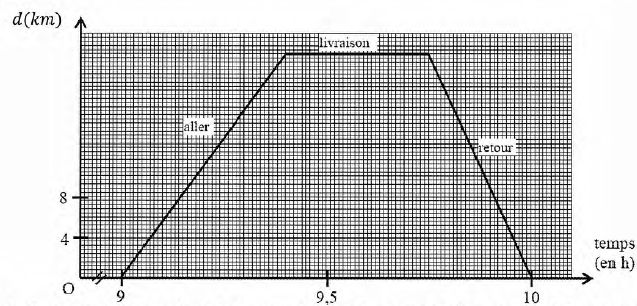
L'artisan part de son atelier à 9h pour se rendre à une boutique et
quand il revient à son atelier, il est 10 h. L'atelier et la boutique
sont distants de 22 km.
1) Calculer la vitesse moyenne ( km/h)pour le trajet aller.
2) Calculer la vitesse moyenne ( km/h) pour le trajet retour.
3) Déterminer graphiquement le temps d'arrêt ( en minute ) nécessaire à la livraison.
|
|
Exercice 2.
On
étudie le déplacement d'un train entre les gares de Montréjeau et de
Saint-Gaudens. La distance entre ces deux gares est de 20 km. Le trajet
dure 15 min et se décompose en trois phases. Dans sa première phase, le
train met 2 min pour parcourir 1,5 km, au bout des deux minutes il
atteint la vitesse constante de 90 km/h et la conserve pendant 10
minutes. On donne la représentation de la vitesse en fonction du temps.
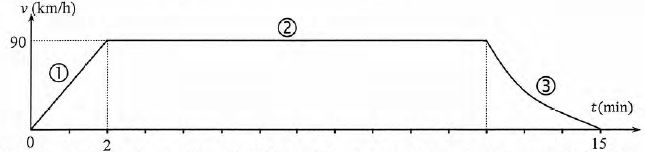
1. Compléter à l'aide du graphique le tableau ci-dessous en justifiant la réponse.
|
Phase 1
|
Phase 2
|
Phase 3
|
Mouvement uniformément accéléré
|
x |
|
|
Mouvement ralenti
|
|
|
x |
Mouvement uniforme
|
|
x |
|
Justification
|
Entre 0 et 2 min, la vitesse et le temps sont proportionnels.
La courbe v(t) est un segment de droite.
|
La vitesse est constante
|
La vitesse diminue
|
2. Exprimer la durée totale du trajet en heure.
3. Calculer la vitesse moyenne du train entre les deux gares en km/h.
Sur lequel de ces deux exercices porterait votre choix ? Justifier. Rédiger un corrigé en précisant les capacités et les connaissances évaluer.
L'exercice
2 permet d'identifier un mouvement à partir d'un enregistrement,
d'effectuer un calcul de vitesse moyenne ; l'exercice 1 permet de
distinguer l'état de repos du mouvement et de faire un calcul de
vitesse moyenne.
L'exercice 2 permet de décrire différents mouvements d'un véhicule.
Question
|
Réponse
|
Capacité et connaissance évaluées
|
1
|
voit tableau ci-dessus
|
Identifier la nature d'un mouvement à partir d'un graphique.
Connaître la nature de différents mouvements : uniforme, uniformément varié.
|
2
|
15 minutes ou 1/4 = 0,25 heure.
|
Savoir convertir des temps en heures et minutes
|
3
|
20 / 0,25 = 80 km/h
|
Savoir calculer une vitesse moyenne
|
|
|



