|
|
|
|
La
pompe à chaleur est une machine thermique qui fait subir un certain
nombre de transformations à un fluide. Une pompe à chaleur permet,
grâce à un apport d'énergie sous forme de travail W, d'extraire une
énergie sous forme de chaleur Q1 à une source
froide de température T1 et de restituer une
énergie sous forme de chaleur Q2 à la source
chaude de température T2, un local à chauffer
par exemple.
Le fluide subit deux transformations isobares aux cours desquelles les
échanges thermiques avec les sources froide et chaude se produisent. On
se place dans cette étude dans le cas de transformations réversibles.
Enoncer
le premier principe de la thermodynamique.
Un système fermé n'échange pas de
matière avec l'extérieur. Le
premier principe traduit la conservation de l'énergie totale
d'un système. Soit
un système fermé évoluant sur un cycle en recevant de l'extérieur une
quantité de chaleur Q et un travail W (grandeurs algébriques), le
principe de l'état initial permet d'écrire : W+Q = 0
Soit dans ce cas : W + Q1+Q2
= 0.
W >0 ; Q1 >0 et Q2
<0.
Le fluide qui circule à travers le circuit est du 1, 1, 1,
2-tétrafluoroéthane nommé R134a.
Donner
la formule développée du R134a.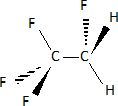
Le R134a comme le chlorodifluorométhane sont aujourd'hui interdits.
Indiquer
l'effet produit sur l'environnement par les chlorofluorocarbures.
Les CFC sont responsables pour une bonne part de la destruction de la
couche d'ozone.
Des produits de remplacement, plus écologiques, sont désormais utilisés
comme fluides frigorigènes.Le R410a est un mélange à 50 % de
difluorométhane et 50 % de 1, 1, 1, 2, 2-pentafluoroéthane.
Indiquer
ce que signifie le pictogramme inscrit sur une bonbonne de
difluorométhane.
Substance inflammable.
On utilise 200 g de 1, 1, 1, 2-tétrafluoroéthane. Le diagramme pression
-enthalpie du R134a est donné. La courbe de saturation limitant le
domaine de coexistence de deux phases est tracé. Le point (1) sur le
diagramme caractérise le fluide à l'entrée du compresseur. On mesure
une pression P1 = 3,00 bar et une température q1
= 5°C.
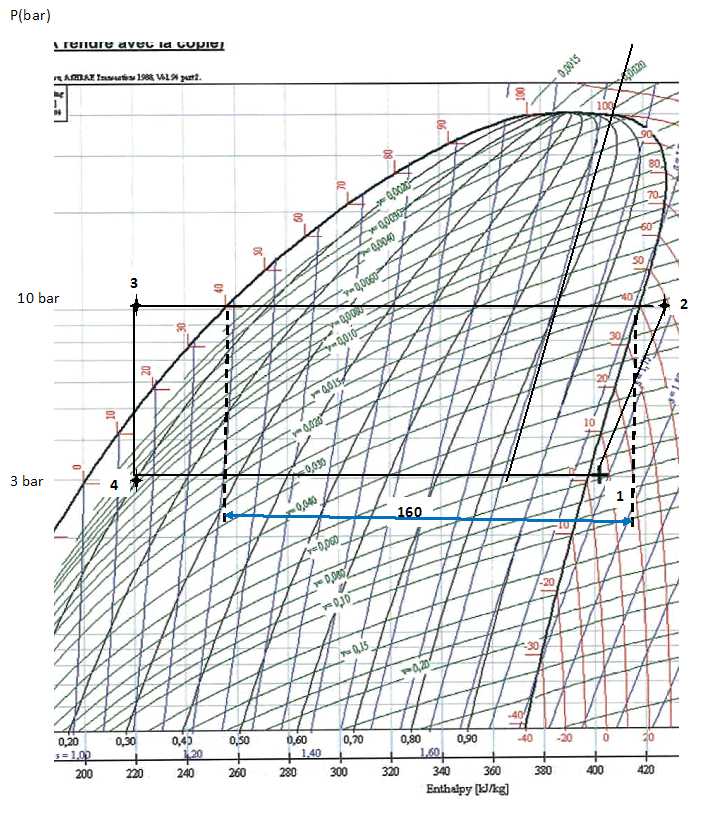
Indiquer la
valeur correspondante de l'enthalpie massique.
L'abscisse du point (1) donne 402 kJ kg-1.
Passage
dans le compresseur.
La transformation est adiabatique réversible. La pression passe de 3,00
bar à 10,0 bar, le travail fourni est W = 25 kJ kg-1.
Le point (2) caractérise le fluide à la sortie du compresseur.
Placer
le point (2), indiquer dans quelle phase se trouve le fluide, donner la
température q2 du fluide.
Le fluide se trouve à l'état de vapeur sèche. Le point (2) est proche
de l'isotherme 50 °C.
Indiquer
le rôle de cette compression et calculer l'énergie fournie sous forme
de travail par le compresseur au 200 g de fluide.
L'abscisse du point (2) est proche de 430 kJ kg-1.
Le compresseur élève la température du fluide en le comprimant.
W = 430-402 = 28
kJ kg-1 soit 28 *0,2 = 5,6 kJ. |
.
|
Passage
dans le condenseur. La transformation est isobare.
L'énergie perdue sous forme de chaleur est de 210 kJ kg-1
et la
température du fluide à la sortie du condenseur est de 15°C. le point
(3) caractérise l'état du fluide à la sortie du condenseur. Placer le
point (3).
Expliquer
les échanges d'énergie sous forme de chaleur entre le fluide et l'air
ambiant.
Les échanges de chaleur s'effectue par conduction et convexion. La
phase liquide du fluide frigorigène apparaît dès que la température de
la surface de refroidissement devient inférieure à la température de
saturation sous la pression de 10 bars. La température du fluide reste
alors constante, égale à la température de condensation. Lorsque tout
le fluide est sous forme liquide, la température de celui-ci diminue de
40°C à 15 °C.
Déterminer
l'énergie sous forme de chaleur cédée par le condenseur.
Q2 = -210*0,2 = -42 kJ.
Déterminer
l'énergie perdue sous forme de chaleur pendant le changement d'état.
Le graphe donne 160 kJ kg-1 soit pour
200 g de fluide : -160*0,2 = -32 kJ.
Passage
dans le détendeur. La transformation est isenthalpe.
Indiquer
le rôle du détendeur.
Le détendeur contrôle l'écoulement du réfrigérant et permet sa détente.
Il évite au compresseur d'aspirer du réfrigérant liquide.
A la sortie le fluide est détendu à basse pression et engendre un début
de vaporisation avec production de froid.
Comment
varie la section de la conduite ?
Le passage offert au liquide est rétréci et débouche coté évaporateur,
dans une tuyauterie de diamètre beaucoup plus important.
Comment
évolue la température ?
Pendant la traversée du détendeur, il n’y a pas d’échange de chaleur
avec l’extérieur (l’enthalpie est la même à l’entrée et à la
sortie du détendeur ). Pour se vaporiser le fluide ne peut prendre la
chaleur utile à sa vaporisation qu’à lui même.Ainsi une partie du
liquide se vaporise pour refroidir l’ensemble.
Le point(4) caractérise le fluide à sa sortie du détendeur. Placer le
point (4).
Ce point est placé sur une ligne indiquant x = 0,10. A quoi
correspond cette valeur ?
10 % du fluide est à l'état gazeux.
Donner
la température q4 du fluide.
0°C.
Passage
dans l'évaporateur.
Expliquer
les échanges d'énergie mis en jeu, indiquer la transformation subie par
le fluide, indiquer comment varie sa température.
Au cours du passage dans
l'évaporateur, le fluide
frigorigène passe de l'état liquide à l'état gazeux : ce phénomène
d'évaporation produit du froid.
Le fluide va se réchauffer tout au long du passage dans l'évaporateur,
captant la chaleur du milieu dans lequel il est (source froide :eau ,ou
air).
Déterminer
l'énergie échangée sous forme de chaleur dans l'évaporateur.
Abscisse du point (4) : 220 kJ k-1 ; 402-220
=182 kJ kg-1. Q1 =
182*0,2 =36,4 kJ.
Vérifier
le premier principe de la thermodynamique pour ce cycle.
Q1 + Q2 + W = 36,4 - 42 +
5,6 =0.
|
|
Le
coefficient d'efficacité de la pompe, noté e, est la valeur absolue du
rapport de l'énergie cédée sous forme de chaleur à la source chaude sur
le travail absorbé.
Exprimer
puis calculer e. Interpréter ce résultat.
e = |-Q2| / W = 42/5,6=7,5. L'efficacité n'a
rien à voir avec un rendement.
A l'aide du second
principe de la thermodynamique, pour un cycle réversible, montrer
que le coefficient d'efficacité s'exprime par e = T2/(T2-T1),
expression dans laquelle T1 est la température
de la source froide en kelvin et T2 celle de la
source chaude en kelvin.
Second principe : Q1/T1
+ Q2/T2 = 0 sur un cycle
réversible ; premier principe Q1 +
Q2 + W = 0 sur le cycle.
Q1/T1
= -Q2/T2
; 0 ; Q1/Q2
= (- T1)/T2 ;
(Q1+Q2)/Q2
=(-T1
+ T2 )/T2 ; -W / Q2 = (-T1 + T2 )/T2
; -Q2 / W = T2 /(T2-T1).
Indiquer
dans quelle condition une pompe à chaleur est la plus efficace.
Une pompe à chaleur est la plus efficace si la différence T2-T1
est faible.
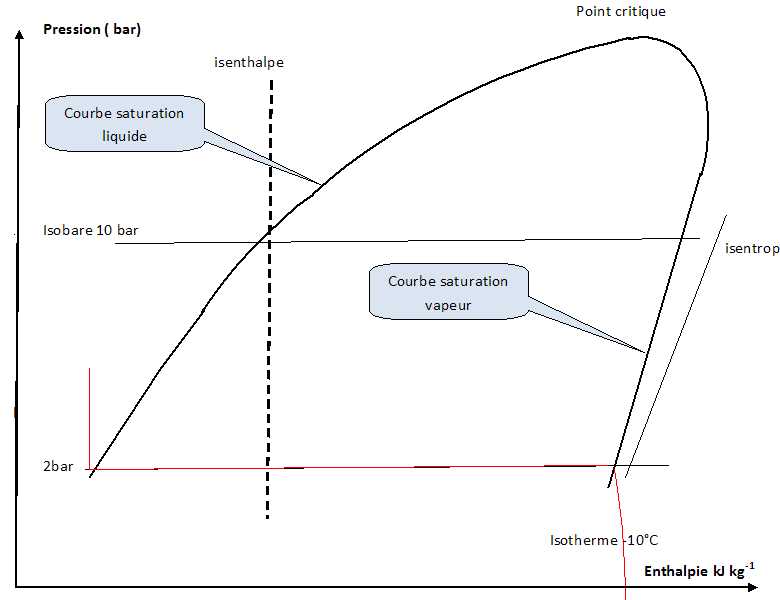
A l'aide du diagramme pression - enthalpie, il est possible de
déterminer les valeurs des pressions de vapeur saturante pour
différentes températures.
Indiquer
la valeur de la pression de vapeur saturante pour -10°C.
2,0 bar.
Le rapport g
des chaleurs massiques à pression constante Cp
et à volume constant Cv est g = 1,22.
En utilisant l'équation des gaz parfaits P V = m RS
q
avec :
m : mase du gaz ( kg) ; RS constante
thermodynamique du gaz R124a : 81,485 J kg-1K-1
; q :
température en kelvin ; P : pression (Pa) ; V : volume (m3).
Calculer
le volume du fluide au point (1).
V = m RS q
/ P =0,200 *81,485 *(273+5) / (3 105 )=1,51 10-2
~1,5 10-2 m3.
Lors de la transformation (1) ---> (2), le fluide suit la loi PVg =
constante.
Calculer
le volume V2.
P1V1g =P2V2g
; V2g
= P1V1g /P2
; V2 = V1(P1/P2)1/g
=1,51 10-2 (3/10)1/1,22
=5,63 10-3 ~ 5,6 10-3 m3.
Calculer
la température q2.
P2
V2 = m RS q2
=P2 V2 /( m RS)
=10 105 *5,63 10-3 /(0,2
*81,485) =345 K ou 345-273 = 72°C.
Le
résultat obtenu valide-t-il l'hypothèse d'un gaz parfait ? Justifier en
définissant un gaz parfait.
Le résultat obtenu est très différent de q2
( 50°C) : l'hypothèse d'un gaz parfait n'est pas valide.
Un gaz parfait est un gaz dans lequel les interactions entre espèces
sont négligeables ; c'est le cas d'un gaz réel sous faible pression et
loin des conditions de condensation.
|
|



