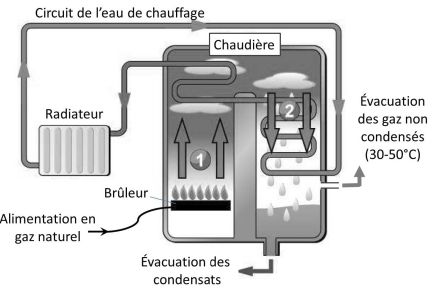
La chaudière à condensation. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Partie 1 : Principe de fonctionnement Dans ce type de chaudière, la vapeur d'eau est transformée en eau liquide Indiquer si le terme condensation est approprié en termes de thermodynamique physique. Justifier. En thermodynamique le terme condensation désigne le passage d'un corps de l'état gazeux directement à l'état solide sans passer par l'état liquide. Le passage d'un corps de l'état gazeux à l'état liquide est appelé liquéfaction. Dans le language courant le terme condensation désigne généralement le passage de l'état gazeux à l'état liquide. Expliquer, en quelques lignes, le principe de fonctionnement de cette chaudière. Dans une chaudière classique, les pertes thermiques se font principalement par les fumées : leur température est élevée et celles-ci contiennent de la vapeur d'eau issue de la combustion du gaz ou du fuel. Le pasage de la vapeur d'eau à l'état liquide restitue de l'énergie ( chaleur latente de liquéfaction ). Le rôle de la chaudière à condensation est de récupérer une fraction de cette chaleur latente de liquéfaction et de la transférer à l'eau du circuit de chauffe. Indiquer en quoi la valeur du rendement ( " jusqu'à 109 %") de cette chaudière peut paraître surprenante. Justifier. Si on prend en compte l'ensemble du cycle énergétique ( suivant le rendement PCS : pouvoir calorifique supérieur ), le rendement d'une chaudière à condensation est de l'ordre de 90 %. Le rendement PCI ( pouvoir calorifique inférieur ) d'une chaudière est le rapport entre l'énergie utile fournie par la chaudière à celle dégagée par la combustion du gaz ou du fuel. Il ne prend pas en compte la chaleur latente de liquéfaction de la vapeur d'eau ni une part de l'énergie des gaz de combustion. Dans les chaudières à condensation , l'apport de chaleur latente de liquéfaction et  la récupération d'une partie de la chaleur des fumées, ajoutés à la quantité d'énergie calorifique, conduit à un rendement PCI compris entre 102 et 109 %. La chaudière condense et évacue beaucoup d'eau en une journée. D'après un chauffagiste cela est dû à la présence de la vapeur d'eau dans le gaz de ville qui alimente la chaudière. Commenter cette affirmation. Cette affirmation est fausse : le gaz de ville contient entre 81 et 97 % de méthane, le reste étant principalement de l'azote. La vapeur d'eau est donc issue de la combustion du méthane.   Exercice bilan sur le rendement et les PCI/PCS du gaz naturel. Préciser la signification du sigle "CNTP" et les valeurs de référence qui y sont usuellement associées. Les conditions normales de température et de pression sont 0°C ou 273,15 K et 1 atmosphère soit 101 325 Pa. Définir, en précisant les grandeurs mises en jeu, le débit volumique. Le débit volumique d'un fluide ( m3 s-1) est le volume ( m3) du fluide s'écoulant durant un temps donné ( s). Rédiger une correction de l'exercice bilan suivant : Le Pouvoir Calorifique Inférieur (PCI) d’un gaz combustible représente la quantité d’énergie libérée par la combustion de 1 m3 de gaz combustible dans les CNTP, l’eau étant considérée à l’état vapeur. Le Pouvoir Calorifique Supérieur (PCS) est déterminé en considérant l’eau produite à l’état liquide. On considère que le gaz naturel est uniquement composé de méthane, de formule CH4. Son Pouvoir Calorifique Supérieur PCS est de 11,3 kW.h/m3. On étudie pour les questions suivantes une chaudière à condensation telle que : - son rendement affiché est r = 109% ; - l’énergie utile fournie à l’eau du circuit de chauffage par mètre cube de gaz naturel consommé est : Eu = 11,1 kW.h / m3 ; - sa puissance utile est P = 21,0 kW. 1. Le rendement est défini par rapport au PCI du gaz naturel. Déterminer la valeur du PCI du gaz naturel. On donne la chaleur latente de liquéfaction de la vapeur d'eau : Lliq= 2,257 106 J kg-1 ou 0,505 kWh m-3. PCI = PCS-Lliq = 11,3-0,505 =10,8 kWh m-3. Déterminer le rendement r’ de la chaudière à condensation par rapport au PCS. Commenter la valeur obtenue par rapport au rendement affiché. r' = énergie utile fournie à l'eau du circuit de chauffe / pouvoir calorifique supérieur . r' = 11,1 / 11,3 =0,98 ( 98 %). Si on prend en compte l'ensemble du cycle énergétique ( suivant le rendement PCS : pouvoir calorifique supérieur ), le rendement d'une chaudière à condensation est de l'ordre de 90 %. 3 - Déterminer la relation littérale entre le débit volumique DV de méthane et la puissance utile P de la chaudière dans le cas d’un fonctionnement ininterrompu. Exprimer la valeur de ce débit volumique DV en m3/h. Energie délivrée par la chaudière en une heure de fonctionnement ininterrompu : 1 * P = 21 kWh. Volume de méthane correspondant : DV=P / Eu = 21,0 / 11,1 = 1,89 m3 h-1. 4 - Pendant 10 minutes de fonctionnement la chaudière consomme un volume de méthane Vméthane de 316 L. Déterminer le volume d’eau condensée Veau lorsque cette chaudière fonctionne pendant 10 minutes. On détaillera les différentes étapes du raisonnement. Données supplémentaires : Volume molaire (CNTP) : Vm = 22,4 L.mol-1 Masse volumique de l’eau liquide : ρeau = 1,00 kg / L Masses molaires M (g.mol-1) : H : 1,0 ; C : 12,0 ; N : 14,0 ; O : 16,0. CH4(g) + 2O2(g) ---> CO2(g) + 2H2O(g). Quantité de matière de méthane : n = Vméthane / Vm = 316/22,4 =14,107 mol. Quantité de matière d'eau : 2 n = 2*14,107 =28,214 mol Masse d'eau : m = 2n M(H2O) = 28,214*18 ~508 g ou 0,508 L. . Premère approche de la différence entre chaleur et température. Beaucoup de recherche en didactique des sciences montrent que les élèves ont des difficultés avec les concepts de chaleur, température et énergie. Il est donc proposé aux élèves de seconde professionnelle, une expérience simple utilisant l'ébullition de l'eau afin de les aider à différencier chaleur et température.  Décrire cette expérience à l’aide d’un schéma légendé et accompagné d’un texte expliquant en quoi elle permettrait de différencier chaleur et température pour les élèves. Placer de l'eau du robinet dans une casserole est chauffer l'ensemble jusqu'à ébullition tout en relevant la température. Laisser ensuite refoidir l'ensemble tout en relevant la température. Lors du chauffage l'eau et la casserole reçoivent de l'énergie : la température de l'ensemble augmente. Lors de l'ébullition, l'eau reçoit de l'énergie : sa température reste constante mais on observe le passage du liquide à l'état de vapeur d'eau. Lors du refroidissement l'eau et la casserole cède de l'énergie à l'air ambiant : la température de l'eau diminue. Le document suivant présente plusieurs observations et réactions d’élèves lors de la réalisation de l’expérience. « Ce n’est pas possible, le thermomètre ne fonctionne pas correctement » (R1) « Si on chauffe plus fort pendant l’ébullition, la température sera plus grande » (R2) « 100°C est la température la plus haute possible pour l’eau » (R3) « La température ne bouge pas parce que la chaleur part dans les bulles de vapeur » (R4) « L’eau ne peut pas stocker plus de chaleur, la chaleur en plus part sur les côtés » (R5) Indiquer, pour chacune de ces réactions (R1 à R5), si elle est correcte ou non. Proposer, le cas échéant, des régulations (commentaires, illustrations expérimentales) permettant à l’enseignant d’infirmer les conclusions des élèves. R1 et R2 sont fausses : le changement d'état d'un corps pur s'effectue à température constante. R3 est fausse si on apporte pas de précision : sous pression atmosphérique, 100°C est la température la plus haute pour l'eau à l'état liquide. Dans un auto-cuiseur, la pression est supérieure à 1 bar et  à 110°C l'eau est encore liquide. R4 est inexacte : le changement d'état physique nécessite un apport d'énergie. R5 : le liquide reçoit de l'énergie et l'agitation des molécules d'eau augmente. Indiquer, en utilisant le premier principe de la thermodynamique, si la chaleur est une forme particulière d’énergie ou un processus particulier de transfert d’énergie. Au cours d'une transformation d'un système fermé, la variation d'énergie du système est égale à la quantité d'énergie échangée avec le milieu extérieur, sous forme de chaleur ou de travail. La chaleur est donc un mode de transfert d'énergie. Proposer une définition de la température que pourrait donner un physicien. La température est une fonction croissante de l'agitation thermique des particules. La température est directement liée à l'énergie cinétique moyenne des constituants microscopiques de la matière ; à l'échelle macroscopique, la température est la manifestation  des mouvements de ces particules. Etude du niveau sonore de la chaudière en fonctionnement. Nommer l'appareil qui permet de mesurer un niveau sonore. Le sonomètre permet de mesurer un niveau sonore en dB ( décibel ). Cet appareil de mesure dispose de deux calibres de mesure( dB(A) et dB(C). Préciser la signification de dB et expliquer la différence entre ces deux calibres. Quel est le mieux adapté aux activités expérimentales proposées aux élèves ? Le décibel ( dB), grandeur sans dimension, exprime le rapport des puissances entre une grandeurmesurée et une valeur de référence. Le "dBA"  tient compte de la différence de sensibilité de l'oreille humaine  aux sons de fréquences différentes. Le sonomètre introduit une pondération "A" est donne la mesure en dB(A). Le dB(C) tient compte du fait que l'oreille humaine ne filtre pas les bruits de la même manière selon leur intensité. On utilise le dB(C) lorsque l'oreille est exposée à des volumes sonores supérieurs à 85 dB. Le dB(A) est le mieux adapté aux expériences proposées aux élèves, le niveau sonore restant inférieur à 85 dB. Ecrire en précisant l'unité associée à chaque grandeur, la relation entre le niveau sonore d'intensité acoustique L et l'intensité acoustique I. L = 10 log ( I / I0) avec I0, intensité de référence en W m-2, seuil d'audibilité.  I s'exprime en W m-2 et L est sans unité. Associer aux valeurs de niveau d'intensité acoustique 0 dB, 40 dB, 80 dB, 120 dB et 160 dB, les termes suivants : seuil de la douleur, seuil de risque, seuil d'audibilité, destruction de l'oreille et seuil de séparation " ambiance calme et ambiance génante". En référence au niveau d’intensité acoustique annoncé pour le modèle de chaudière étudié, justifier ou critiquer la phrase : « Elle offre un très bas niveau sonore : 34,1- 46,2 dB ». Cette intervalle 34,1- 46,2 dB correspond à une conversation normale dans un bureau, mais il reste bien supérieur à celui d'une zone calme. Le terme "très bas" n'est pas justifié. Un haut-parleur émet une onde sonore périodique de fréquence f. Le centre du haut-parleur est repéré par le point S. On dispose de deux microphones de centres M1 et M2, tels que les points S, M1 et M2 soient alignés selon l’axe noté (Sx). Chaque microphone est relié à une voie d’un oscilloscope. Les deux microphones étant initialement collés l’un à l’autre, on en éloigne un. M1M2 = 27 cm est la plus petite distance qui permette d’obtenir l’oscillogramme suivant :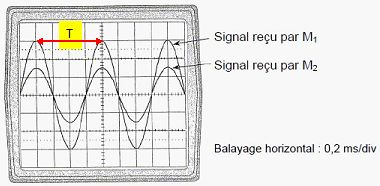. Indiquer s’il s’agit d’un son pur, complexe ou d’un bruit. Justifier. Les courbes sont des sinusoïdes, le son est pur.  Déterminer la période T et la fréquence f du signal observé. Indiquer la (les) grandeur(s) sur l’oscillogramme fourni. T = 4*0,2 = 0,8 ms = 8,0 10-4 s ; f = 1/T = 1/(8,0 10-4) =1,25 103 Hz.  Indiquer si l’on peut dire d’une onde sonore qu’elle est longitudinale. Justifier. Une onde sonore est longitudinale, il s'agit de la propagation d'une variation de pression. La direction de propagation de l'onde est la même que celle de la perturbation. On suppose que l’élongation au centre S de la membrane est de la forme y = ym.sin(2πf.t). Soit un point M situé à l’abscisse x du point S. Écrire l’expression y(x, t) de l’élongation en ce point. Justifier. Le point M reproduit le mouvement de la source S avec un retard q = x/v, v : célérité de l'onde. y(M) = ym.sin(2πf.(t-x/v)) = ym.sin(2π.(f t-x/l)).  En déduire la valeur de la longueur d’onde λ, puis celle de la célérité c du son dans l’air. l =M1M2 = 27 cm ; v = l f = 0,27*1250 =337,5 ~3,4 102 m/s.

Le document suivant présente un questionnaire soumis à des élèves et quelques résultats obtenus concernant la propagation d’un son et l’influence du milieu. Il s’agissait pour le chercheur en didactique d’étudier les conceptions des élèves sur ce thème. On considère quatre tubes : le premier est rempli d’air, le second est rempli d’eau, le troisième est rempli d’acier et dans le quatrième le vide a été fait (il n’y’a rien). À une extrémité de chaque tube, un haut-parleur (H.P.) est branché et à l’autre extrémité se trouve un microphone (M.) relié à un magnétophone. Tous les haut-parleurs, microphones et magnétophones sont identiques. Tous les haut-parleurs commencent à émettre la note « la » au même instant et s’arrêtent au même instant. 1) Quels sont les microphones qui enregistrent un son et quels sont ceux qui n’en enregistrent pas ? Expliquer pour chaque tube pourquoi. 2) Pour les microphones qui enregistrent un son : Commencent-ils à enregistrer un son au même instant ? Oui, pourquoi ? Non, pourquoi ? Classez les microphones par instant d’arrivée du son croissant et justifiez votre réponse. Quelques résultats obtenus pour 108 élèves de troisième, seconde et première scientifique, avant enseignement sur la propagation du son : - Un son peut se propager dans le vide (44%). Exemple : « Oui pour le vide : le son ne rencontre aucune opposition » (réponse R6). - La propagation d’un son est impossible dans un liquide (22%) ou dans un solide (61%). Exemple : « Oui, sauf l’acier plein parce que le son ne pourra pas traverser le tube plein pour être enregistré, et l’eau » (réponse R7). - La vitesse de propagation du son dépend du milieu (76%). Pour beaucoup de ces élèves, un son se propage plus vite dans le vide que dans l’eau ou l’acier. On retrouve ce type de réponse après enseignement (élèves de première et terminale scientifiques, étudiants des deux premières années d’université scientifique) : Exemple : « la vitesse de propagation dépend du milieu. Elle est freinée par les collisions avec les molécules plus ou moins nombreuses du milieu : eau, air, vide (ordre croissant donné pour les vitesses) » (réponse R8). Définir ce qu’on entend, en didactique des sciences, au travers de la notion de « conception » et argumenter autour des difficultés posées, à l’enseignant, par ces « conceptions » dans l’apprentissage des sciences. L'enseignement de la physique se heurte à des conceptions "spontanées"  ( représentations types ) qui peuvent faire obstacle à l'apprentissage  parce qu'elles s'opposent au "bon sens" commun.  Répondre au questionnaire  tel qu’un physicien le ferait. 1) Un son ne se propage pas dans le vide : seul le microphone placé à l'extrémité du tube dans lequel le vide est fait ne perçoit rien. 2) La vitesse du son est d'autant plus grande que la masse volumique du milieu et sa compressibilité sont faibles : Vacier > Veau >Vair. Les microphones ne perçoivent pas le son au même instant. Proposer un libellé (une courte phrase) permettant de caractériser la conception des élèves conduisant aux réponses R6, R7 et R8. "Un son s'accompagne d'un transport de matière". Proposer le moyen qui vous semble le plus efficace pour déconstruire la conception décrite dans la question précédente.Une onde mécanique transporte de l'énergie, sans transport de matière. Un bateau pris dans une houle se déplace verticalement ( son énergie augmente  de l'énergie potentielle mgH ) lors du passage de l'onde, puis il revient à sa position initiale. Le navire ne se déplace pas suivant une direction horizontale.

menu