Système GPS :
satellite en
orbite circulaire, Capes 2014.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
On
se propose d'étudier le mouvement des satellites autour de la terre
dans le référentiel géocentrique, suposé galiléen. On considère la
terre comme une sphère homogène de rayon R, de centre O et de masse M.
On note G la constante de gravitation universelle.
On repère un
point M par ses coordonnées sphériques (r, q, f) dans le référentiel
géocentrique.
Situé
l'époque à laquelle le premier satellite artificiel a été lancé.
Le premier satellite artificiel, Spoutnik1, a été lancé en 1957.
Déterminer
à l'aide de considérations de symétrie la direction du champ
gravitationnel créé par la terre en un point M quelconque de l'espace.
Tout
axe passant par O est un axe de symétrie de la distribution et donc du
champ de gravitation résultant. Ce champ est nécessaitrement radial et
sa valeur ne peut dépendre que de r= OM.
Enoncer le théorème
de Gauss relatif à la gravitation.
Le flux
du champ de gravitation à travers une surface fermée est égal à la
somme des masses intérieures multipliée par - 4pG.
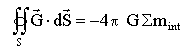
En déduire
l'expression du champ de gravitation créé par la terre en un point
extérieur à celle-ci.
On prend comme surface de
Gauss une sphère de rayon r : sur cette sphère le champ de gravitation
a une norme constante et est colinéaire au vecteur surface.
Pour r supérieur au rayon de la répartition de masse, la somme des
masses intérieures est m1= M.
g(r) 4pr² = -4pGm1.
g(r) = - Gm1/r²
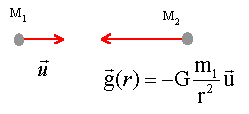
Par suite, le champ
gravitationnel créé à l'extérieur par un corps à distribution de
masse à symétrie sphérique est équivalent à celui d'une mase
ponctuelle, égale à la masse du corps, et située en xon centre.
Quelle
est la force exercée par la terre sur un satellite de masse m en orbite
autour de la terre ?
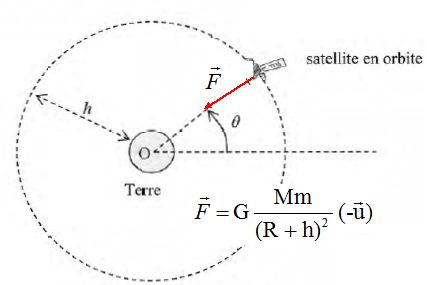
En
déduire que la trajectoire est plane.
Ecrire le théorème du moment cinétique en O : 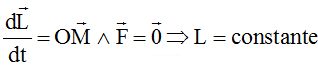
La trajectoire est plane : ce plan contient le point O et le vecteur
force F. Ce
plan est perpendiculaire au moment cinétique.
|
|
|
On suppose que l'orbite du
satellite est circulaire de centre O et que le satellite est situé à
une altitude h = 20,2 103 km. On repère le satellite par des
doordonnées polaires ( r = R+h, q
) dans le plan de la trajectoire.
Exprimer
les composantes de l'accélération du satellite en coordonnées polaires
en fonction de la norme v de la vitesse, de sa dérivée par rapport au
temps dv/dt et du rayon r.

Montrer
que le mouvement du satellite est nécessairement uniforme.
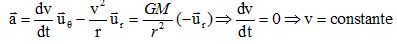
La valeur de la vitesse étant constante, le mouvement est uniforme.
Déterminer
la norme de la vitesse en fonction de G, M et R+h.
v2 = GM/r = GM((R+h) ; v = (GM/(R+h))½.
En un point de la surface de la terre, on assimile de champ de
pesanteur, d'intensité g, au champ de gravitation.
Exprimer v en
fonction de g et R+h.
g = GM/R2 ; v = (gR2/(R+h))½
= R(g/(R+h)½.
A.N : R = 6,37 103
km ; g = 9,81 m s-2.
v = 6,37 106 (9,81 /
(6,37 106 +20,0 106))½
=3,87 103 m /s.
|
.
|
|
Relier
la période de rotation du satellite T aux paramètres G, M et R+h.
Le satellite décrit la circonférence 2p(R+h)
à la vitesse v en T secondes.
v = 2p(R+h)
/ T ; v2 = 4 p2(R+h)2/T2.
or v2 = GM / (R+h) : 4 p2(R+h)3/T2
= GM ou T2 = 4 p2(R+h)3/(GM).
( 3è loi de Kepler).
Enoncer la 3è loi de
Kepler et situer l'époque où a vécu J. Kepler.
Pour
toutes les planètes du système solaire, dans le référentiel
héliocentrique, le rapport entre le carré de la période de révolution
d'une planète autour du soleil et le cube de son demi-grand axe orbital
est égal à une même constante. J. Kepler ( 1571 - 1630).
On souhaite que la période de révolution des satellites du système GPS
soit égale à la moitié de la durée du jour solaire.
Evaluer
l'altitude des satellites de la constellation GPS.
v = 2p(R+h) / T
; R+h = vT /(2p) =3,87
103 *12*3600 / 6,28 =2,66 107 m ; h = 2,66
107 -6,37 106 =2,03 107 m = 2,03 104
km.
Montrer que la force
de gravitation est conservative.
L"énergie
totale d'un système soumis à une force conservative est constante. Il
suffit alors que cette force dérive d'un potentiel, noté Ep.
Ep = -GMm/r. F = dEp/dr =
GMm/r2. L'origine de l'énergie potentielle de gravitation
est prise à l'infini.
On note Ec l'énergie cinétique du satellite.
Vérifier que 2Ec+Ep=0.
Ce résultat est connu sous le nom de théorème de viriel.
v2 = GM/r ; 2Ec+Ep
= mv2 -GMm/r = GMm/r-GMm/r =0.
D'un
point Q, situé sur terre, dans le plan de l'orbite du satellite P, on
ne peut observer ce satellite que pendant l'intervalle de temps t entre son apparition à
l'horizon, en A, et sa disparition, en B.
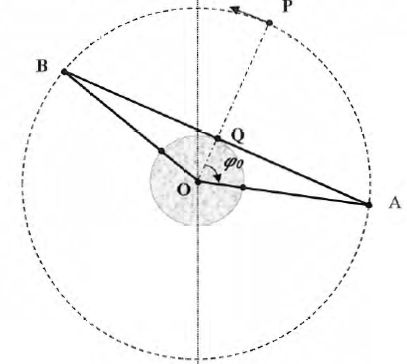
Déterminer
géométriquement l'expression de l'angle f0.
cos f0 = OQ / OA = R /
(R+h). f0
=arcos(R / (R+h)) =arcos(6,37 /
(6,37+20,2)) =0,240 ; f0 =76,1° ou 1,33 rad.
En déduire la
longueur de l'arc AB.
Longueur de l'arc AB : arc(AB)=2f0 (R+h) avec f0 en radians.
Relier
t à la longueur de
l'arc AB, T et R+h.
2p(R+h) = v T ; arc (AB) =2f0
(R+h) = v t = 2p(R+h) t / T ; t = f0 T / p.
En
déduire t en fonction de h, g
et R.
La troisième loi de Kepler
conduit à T = 2p(R+h)1,5
/ (Rg½ ) ; t = f0 T / p = 2 f0 (R+h)1,5 / (Rg½ ).
Vérifier
la dimension de t.
(R+h)1,5
s'exprime en m1,5 ; g½ s'exprime en m½s-1
; (Rg½ ) s'exprime en m1,5s-1
; (R+h)1,5 / (Rg½ ) s'exprime en seconde.
A.N : t =2*1,33
*(6,37 106 +20,2 106)½ / (6,37 106
*9,81½) =1,83 104 s ou 5,07 h.
Calculer le rapport T/t.
T/t=12/5,07
=2,36.
Pour les besoins du système GPS, on dispose régulièrement sur une même
orbite un ensemble de satellites identiques, appelés " train de
satellites".
Calculer
le nombre minimal de satellites nécessaires pour former un "train" afin
que tous les points au sol , dans le même plan de l'orbite, voient au
moins un satellite à tout instant.
T/t=2,36
: un train doit être formé d'au moins trois satellites.
|
Supposons
maintenant qu'un satellite est visible s'il est à plus de a0 = 30 ° au dessus de
l'horizon. Ainsi le satellite est visible depuis Q lorsqu'il est entre
A' et B'.
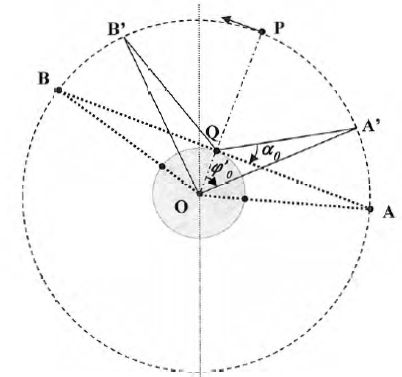
En
projetant A' sur OP, déterminer une relation liant f'0, a0, R et R+h.
Soit H la projection de A' sur OP : sin f'0 = HA' /OA'=HA' /
(R+h)
; tan
a0
=QH/HA' ; sin
f'0
tan
a0 =QH/(R+h).
cos f'0 =OH/(R+h) = (R+QH)
/ (R+h) ; (R+h)cos
f'0 = R+QH
=R+(R+h)sin
f'0
tan
a0 ;
on pose h = R/(R+h).
cos
f'0 =h+ sin
f'0
tan
a0.
Montrer
que u = cos f'0
vérifie pour a0 = 30°, l'équation
: u2-1,5 hu+0,75h2-0,25 = 0.
tan 30° =0,577 ; u = h+ 0,577 sin
f'0
; u
= h+ 0,577(1-u2)½
; (u-h)2 = 0,5772(1-u2).
u2+h2-2uh =0,333 -0,333 u2.
1,333
u2 +h2-2uh =0,333 ; u2
-1,5
uh +0,75 h2-0,25 =0.
Résoudre
cette équation et en déduire la valeur de f'0. h = 6,37 / (20,2+6,37) = 0,24.
u2-0,36 u-0,207 = 0. D = 0,362+4*0,207=0,9576
; u1 =(0,36+0,98) /2 = 0,67 et u2
=(0,36-0,98) /2 = -0,31.
f'0 =
48° ( 0,84 rad ) ou 108°. 108 ° ne peut convenir ( voir figure
ci-dessus ).
Quelle
est la nouvelle durée de visibilité t' ? Quel est alors le nombre
minimal de satellites dans un "train" ?
t' = f'0 T / p = 0,84 *12/3,14 = 3,2 h : un
"train " doit compter au minimum 4 satellites.
Dans la constellation du système GPS, les 24 sattellites utilisés
évoluent sur 6 plans orbitaux ayant une inclinaison d''environ 55° sur
l'équateur. Ces orbites sont séparées de 60° les unes par rapport aux
autres et contiennent un train de 4 satellites.
Citer le nom du projet européen de positionnement par satellite et décrire l'état actuel de son fonctionnement.
Le
projet Galiléo : 4 satellites ont été lancés ; les premiers services
seront disponibles en 2014 ; le système devrait être finalisé en 2020.
|
|