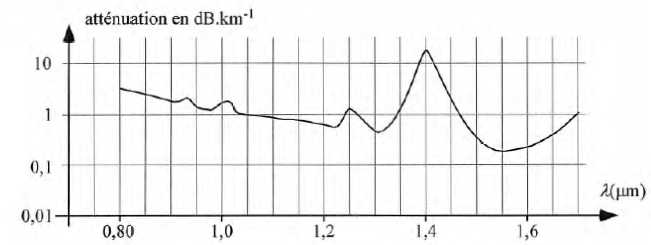
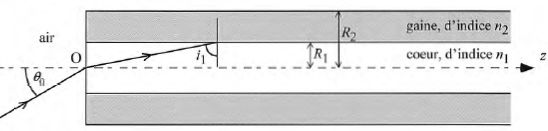
Fibre optique à saut d'indice, ouverture numérique, dispersion, atténuation Capes 2014. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Considérons une fibre optique dont le coeur est un cylindre circulaire d'axe Oz, de rayon R1 et d'indice optique n1. O est le centre de la face d'entrée de la fibre. La gaine  est également d'axe Oz, d'indice n2, de rayon intérieur R1 et de rayon extérieur R2. Les indices vérifient l'inégalité n1>n2. Une telle fibre est dite à saut d'indice. Soit un rayon lumineux arrivant en O à l'entrée du coeur de la fibre. Dans l'air il est incliné d'un angle q0 par rapport à l'axe Oz. Après réfraction dans le coeur de la fibre, le rayon arrive à l'interface entre le coeur et la gaine, avec un angle d'incidence i1. L'indice de l'air est égal à 1. Tous les angles intervenant dans cette partie sont compris entre 0 et ½p. Notion d'ouverture et de modes. Etablir lune relation entre les angles i1, q0 et les indices des milieux. Réfraction en O : nair sin q0 = n1 sin r avec r + i1 = 90° soit sin r = cos i1. sin q0 = n1 cos i1. Quelle est la condition portant sur sin i1 et les indices des milieux pour qu'il y ait réflexion totale à l'interface coeur-gaine ? Cas limite de la réflexion totale : n1 sin i1 lim = n2 ; sin i1 lim = n2 /n1. sin i1doit être supérieur ou égal à n2 /n1. On appelle ouverture numérique de la fibre ON = (n12-n22)½. Quelle est en fonction de ON, la valeur maximale q0 max de l'angle q0 au delà de laquelle il n'y a plus réflexion totale à l'interface coeur-gaine ? A.N : n1 = 1,48, n2 = 1,46. sin i1 lim = n2 /n1 ; sin q0 max = n1 cos i1 lim. sin2 i1 lim =(n2 /n1)2 ; cos2 i1 lim = sin2 q0 max / n21 ; sin2 i1 lim +cos2 i1 lim =1. 1 = (n2 /n1)2 + sin2 q0 max / n21 ; n21 =n22+sin2 q0 max. n21 -n22=sin2 q0 max = ON2. sin q0 max = ON. ON = (1,482-1,462)½ =[(1,48+1,46)(1,48-1,46)]½ =0,2425 ; q0 max =14,0°.   La détermination des différents modes de propagation des ondes électromagnétiques dans une fibre optique fait appel aux équations de Maxwell et aux équations de propagation qui en découlent. Les solutions rigoureuses s'écrivent au moyen des fonctions de Bessel. Il est toutefois possible d'obtenir des solutions approchées, et d'appréhender la notion de modes avec un formalisme allégé, en s'appuyant sur des considérations simples d'optique ondulatoire. 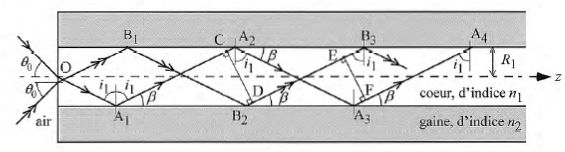Considérons un plan de symétrie de la fibre contenant l'axe Oz. Soient deux rayons lumineux se propageant dans ce plan, au coeur de la fibre optique, l'un repéré par une simple flèche, l'autre par une double flèche. Les ondes associées à ces deux rayons sont monochromatiques, cohérentes, de longueur d'onde dans le vide l. Elles subissent des réflexions totales aux interfaces coeur-gaine, c'est à dire aux points A1, A2, A3 etc pour le rayon repéré par une simple flèche, et aux points B1, B2 etc pour le rayon repéré par une double flèche. Soient C et D les points des rayons A1A2 et B2B3 se trouvant dans un même plan orthogonal aux deux rayons. Soient E et F les points des rayons A3A4 et B2B3 se trouvant dans un même plan orthogonal aux deux rayons. Dans un premier temps, on ne prend pas en compte les éventuels déphasages dus aux réflexions. Exprimer la différence de chemin optique d entre les deux rayons allant du plan contenant Cet D au plan E et F. La différence sera choisie de telle sorte que d soit positif. d=n1(CA2 +A2A3+A3F -DE). Soient A'1 et A'3 les projetés orthogonaux des points A2 et A3 sur le rayon B2B3. Exprimer la différence de marche en fonction de A2A3, A'2A'3 et n1. d=n1(DA'2 +A2A3+A'3E -DE) = n1(A2A3-A'2A'3). Montrer que cette différence de marche peut s'écrire d = 4R1 sin q0. A'2A'3 = B2B3-B2A'2-A'3B3 =A2A3-2R1sinß-2R1sinß. d=n14R1sinß ; réfraction en O : sin q0 = n1 sin ß ; par suite : d=4R1sin q0. On suppose que pour que la propagation soit possible, cette différence de marche doit être égale à un nombre entier de fois la longueur d'onde l. Commenter cette hypothèse et en déduire la condition (C1) associée en introduisant un entier naturel m, que l'on nommera " indice de mode". Les ondes qui se propagent dans la fibre sont cohérentes et synchrones. Leur superposition conduit à des interférences. Celles-ci sont constructives si la différence de marche est un multiple de la longueur d'onde. d = m l ;  4R1sin q0 = m l. On notera q0 m et ßm les angles q0 et ß associés au mode m. Quelle inégalité doit vérifier m compte tenu de l'ouverture numérique ? sin q0 max = ON = (n12-n22)½ ; 4R1sin q0 m = m l ; sin q0 m =m l /(4R1). m=0 conduit à q0 0 =0 ; valeur maximale de m : partie entière de 4R1sin q0 max / l = 4R1(n12-n22)½ /l. Montrer que pour n1 = 1,447 et n2 = 1,443, R1 = 3,50 µm et l = 1,55 µm, seul le mode m=0 est possible. La fibre est dite monomode. sin q0 max = ON = (1,4472-1,4432)½ =0,1075 ; Valeur maximale de m : partie entière de 4*3,50 *0,1075 / 1,55 =0. On tient compte à présent des déhasages dus aux réflexions. Lorsqu'une onde lumineuse se propageant dans un milieu d'indice na rencontre un dioptre séparant le milieu d'indice na d'un milieu d'indice nb,  à quelle condition la réflexion sur le dioptre s'accompagne-t-elle d'un déphasage de p ? Si n1 est supérieur ou égal à n2, il n'y a pas de déphasage ; si n1 est inférieur ou égal à n2, il y a un déphasage de p. La condition C1 est-elle modifiée si l'on prend en compte le déphasage éventuel lié à la réflexion ? La réflexion totale peut se produire si n2 < n1. Dans ce cas il n'y a pas de déphasage lié à la réflexion et la condition C1 reste inchangée. . Dispersion. Il existe plusieurs types de dispersion au sein d'une fibre optique. Dispersion intermodale. On considère une fibre multimode d'axe Oz, de longueur L, avec un coeur de rayon R1 et d'indice optique n1, et une gaine d'indice n2<n1. Supposons qu'une diode laser émette une impulsion lumineuse de longueur d'onde dans le vide l pendant une durée t0. Les caractéristiques de la fibre sont telles qu'il existe N+1 modes, d'indices compris entre 0 et N. Pour le mode d'indice m; ßm = arcsin(ml/(4n1R1)). Montrer que pour une fibre optique de longueur L, la distance parcourue par la lumière pour le mode m est L / cos ßm. En déduire l'expression du chemin optique dans la fibre. Pour le mode m, la lumière suit le trajet O, A1m, A2m, A3m ... tel que  OA1m = OH  / cos ßm avec H projection orthogonale de A1m sur l'axe Oz. La longueur d'un tel trajet est donc : L / cos ßm. Le chemin optique vaut n1L / cos ßm. Quel est l'indice du mode dont la durée de la propagation le long de la fibre est le plus court ? La durée la plus courte correspond au chemin optique le plus petit, soit pour la plus grande valeur de cos ßm : cos ßm =1 ; ßm =0 ; m = 0. On note Dtm la durée de la propagation des signaux lumineux le long de la fibre de longueur L pour le mode m, et c la célérité de la lumière dans le vide. Exprimer Dtm en fonction de ßm. Dtm  = L / (v cos ßm) avec v = c/n1. Dtm  = n1L / (c cos ßm). On note respectivement DtMin  et DtMax  les durées de propagation correspondant aux modes pour lesquels cette durée est respectivement la plus courte et la plus longue. Exprimer  DtMin  et DtMax  en fonction de L, n1, R1, N, l et c. DtMin  = n1L / c. DtMax  =n1L / (c cos ßm) avec sin ßm= sin q0m/n1 = Nl/(4R1n1). cos2 ßm = 1 -sin2 ßm =1-(Nl/(4R1n1))2. DtMax  =n1L [1-(Nl/(4R1n1))2]-½ / c = 4n21LR1[(4R1n1))2-(Nl)2]-½ / c = n1L/c (4R1n1 [(4R1n1))2-(Nl)2]-½). La figure ci-dessus illustre de façon schématique la dispersion intermodale. Une impulsion lumineuse rectangulaire de durée t0 est émise en z=0, entre t=0 et t=t0. En raison de l'existence des N+1 modes, lorsque l'impulsion arrive au bout de la fibre en z=L, elle est allongée et déformée. Elle démarre à t = t1, atteint sa valeur maximale à t = t2, garde cette valeur jusqu'à t = t3, puis prend fin à t = t4. On suppose qu'il n'y a aucune autre source de dispersion. Interpréter la forme de l'impulsion en z = L. Les ondes émises à la date t=0 qui empruntent le trajet le plus court, sortent de la fibre à la date t1 = DtMin ; Les ondes émises à la date t=0 qui empruntent le trajet le plus long, sortent de la fibre à la date t2 = DtMax ; l'amplitude en sortie est alors maximale jusqu'à la date t3 = DtMin +t0. L'amplitude décroît ensuite jusqu'à la date t4 = DtMax +t0. Exprimer le temps de montée  tm = t2-t1 en fonction de DtMin et DtMax. tm = t2-t1=DtMax -DtMin. Exprimer les instants t3 et t4 puis le temps de descente  td = t4-t3 en fonction de DtMin et DtMax et t0. td = t4-t3= DtMax +t0-(DtMin +t0)==DtMax -DtMin. On note tL la durée de l'impulsion en bout de fibre. On définit l'élargissement de l'impulsion par unité de longueur Dt/L = (tL-t0) / L. Montrer que cette quantité a pour expression : Dt/L = n1/c {(4R1n1 [(4R1n1))2-(Nl)2]-½)-1}. Dt/L =(DtMax  - DtMin ) /L =n1/c (4R1n1 [(4R1n1))2-(Nl)2]-½) - n1 / c. Cette quantité est souvant donnée en ns km-1. Donner sa valeur numérique dans cette unité. n1 = 1,48 ; N = 15 ; R1 = 25,0 µm ; l = 1,55 µm et c = 3,00 108 m/s. [(4R1n1))2-(Nl)2]-½=[(4*25,0 10-6*1,48))2-(15*1,55 10-6)2]-½=6,842 103 m-1. 4R1n1 [(4R1n1))2-(Nl)2]-½)-1=4*25,0 10-6*1,48*6,842 103 -1 =1,257 10-2. Dt/L =1,48/(3,00 108 )*1,257 10-2= 6,20 10-11s m-1 = 6,20 10-11*109 / 10-3 ns km-1 =62,0 ns km-1. L'élargissement des impulsions impose une limite pour le débit lors de la transmission d'informations numériques par fibre optique. En efffet, si la période d'horloge, c'est à dire la durée entre chaque bit, est TH, l'information est impossible à récupérer en bout de fibre si l'élargissement des impulsions devient comparable à tH. En utilisant les valeurs numériques précédentes, et en prenant comme critère de transmissibilité de l'information un élargissement d'impulsion inférieur ou égal à 0,25 TH, calculer en Mbits/s le débit maximal admissible Qmax dans une fibre de longueur 1 km. Elargissement de l'impulsion au bout de 1000 m :  6,20 10-11*103 <= 0,25 TH. TH >= 6,20 10-8/0,25 ; TH >=2,48 10-7 s. Qmax =1/TH = 1/(2,48 10-7 ) =4,03 106 bits/s = 4,03 Mbits/s. Soit Q'max le débit maximal admissible dans une fibre optique de longueur L = 20,0 km. Quel est le lien entre Qmax et Q'max ? Q'max = Qmax / 20. En pratique, la dispersion intermodale limite l'utilisation des fibres optiques multimodales à saut d'indice aux réseaux locaux.Les liaisons internationales ou nationales à haut débit nécessitent des fibres à gradient d'indice ou des fibres à saut d'indice monomodales. Dispersion intramodale. Dans les fibres monomodes, utilisées pour les liaisons à haut débit sur de grandes distances, la dispersion est due, d'une part au phénomène de guidage dans le coeur, et d'autre part à la dépendance de l'indice du milieu constituant le coeur de la fibre, vis à vis de la longueur d'onde lumineuse. La dispersion due au guidage, dans une fibre monomode, fait appel à un traitement mathématique lourd, et ne peut pas s'appliquer avec un modèle utilisant les rayons lumineux. Notons D le coefficient de dispersion intramodale dans une fibre monomode. Ce coefficient est définit par D = 1/L dtg/dl où dtg(l) est la durée de propagation dans la fibre de longueur L, à la vitesse de groupe vg, pour la longueur d'onde l. En notant respectivement Dgd et Dm les coefficients de dispersion dus au guidage et au milieu, on peut écrire D = Dgd + Dm. 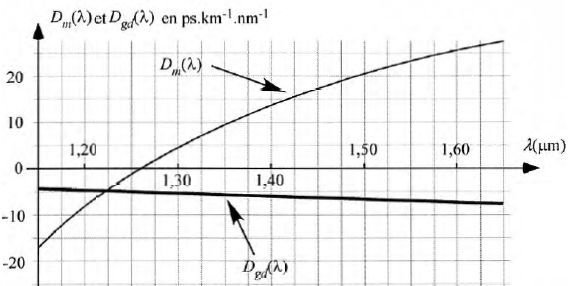Montrer qu'il existe une longueur d'onde particulière l1 pour laquelle la dispersion intermodale est nulle. Evaluer graphiquement sa valeur numérique. Pour une longueur d'onde supérieure à 1,26 µm, Dm(l) est positive et croissante tandis que Dgd(l) est négative et décroissante. La somme de ces deux termes peut donc être nulle pour une valeur particulière de l. Nous constatons graphiquement que le coefficient de dispersion intramodale est nul pour l1 ~1,31 µm. Pour une longueur d'onde l = 1,55 µm, évaleur graphiquement la valeur de la dispersion intramodale. En déduire l'écart Dtg de durée de propagation dans une fibre de longueur 100 km, si la source lumineuse utilisée a une longueur d'onde centrale l = 1,55 µm et une largeur spectrale Dl = 1,00 nm. Dm(1,55) = 23 ps km-1 nm-1 ; Dgd(1,55) = -7 ps km-1 nm-1 ; D = 23-7 = 16 ps km-1 nm-1. D = 1/L Dtg/Dl donne : Dtg = D L Dl = 16 *100 *1,00 = 1,6 103 ps = 1,6 ns. Si on considère que l'information est convenablement transmise tant que Dtg est inférieur ou égal au quart de la durée TH d'une période d'horloge, calculer en Mbits / s le débit maximal admissible Q"max dans cette fibre de longueur 100 km. TH >= 4*1,6 10-9 s. Q"max = 1/TH =1/(6,4 10-9) =1,56 108 ~1,6 108 bits/s = 1,6 102 Mbits / s. En pratique, il est possible d'ajuster la longueur d'onde pour laquelle la dispersion intramodale est quasiment nulle, en donnant à la fibre un profil d'indice particulier. Toutefois, il existe un autre phénomène de dispersion, appelé dispersion de polarisation, qu'on ne peut parvenir à éliminer, et qui limite les débits des propagations à très grandes distances.  .

Atténuation. L'atténuation provient à la fois de l'absorption et de la diffusion des ondes lumineuses par la matière qui constitue les fibres. La plupart des fibres sont réalisées en silice, relativement pure, dont l'absorption ne devient sensible que pour des longueurs d'ondes supérieures à 1,6 µm. Les impuretés, quasiment impossible à éliminer, contiennent généralement des liaisons OH. Rappelons que la liaison OH présente un pic d'absorption dans l'infra-rouge, pour une longueur d'onde d'environ 1,4 µm. La silice se présente dans les fibres sous forme amorphe. Les irrégularités qui en résultent sont responsables d'une diffusion de la lumière, de type diffusion de Rayleigh. Rappelons que la diffusion de Rayleigh est responsable de la couleur bleue du ciel et de la couleur rouge-orangée du soleil couchant : lorsqu'un rayon lumineux venant du soleil rencontre l'atmosphère terrestre, une partie de la lumière est diffusée latéralement, beaucoup plus dans le domaine du bleu que dans le domaine du rouge, qui est ainsi mieux transmis. La figure suivante donne l'allure de l'atténuation ( en dB km-1) en fonction de la longueur d'onde lumineuse pour une fibre optique ordinaire. En utilisant les informations du paragraphe précédent, interpréter la forme de cette courbe. L'absorption est faible pour des longueurs d'ondes inférieures à 1,6 µm. Le pic à 1,4 µm est du à l'absorption des liaisons OH présentes dans les impuretés. Les petites irrégularités sont dues à la forme amorphe de la silice qui constitue les fibres. Une des causes de l'atténuation est la diffusion Rayleig : tout atome diffuse nécessairement la lumière. On montre que la puissance diffusée est proportionnelle à 1 / l 4. Les longueurs d'onde de l'infrarouge sont supérieures à celle du visible et de l'UV) : dans l'IR la puissance diffusée sera plus faible que dans le visible ou l'UV. Evaluer en le justifiant quelles sont les deux longueurs d'onde les plus appropriées à la transmission d'informations dans cette fibre. L'atténuation doit être minimale pour une bonne tranmission: l = 1,32 µm et l = 1,55 µm. Pour une longueur d'onde l = 1,55 µm, l'atténuation est de 0,2 dB km-1. Quel pourcentage de la puissance injectée à l'entrée de la fibre parvient à une distance de 100 km ? Atténuation sur une longueur de 100 km : 0,2*100 = 20 dB. -20 = 10 log (puissance perdue / puissance d'entrée)  ; puissance perdue = puissance d'entrée / 100. Puissance de sortie = 0,99 fois la puissance d'entrée.

menu