Transmission de signaux numériques : ligne bifilaire en cuivre, Capes 2014. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Les lignes téléphoniques, installées depuis de nombreuses décennies, initialement pour assurer la transmission de signaux analogiques de la téléphonie, contribuent aujourd'hui beaucoup à la transmission de signaux numériques, pour l'internet, la télévision et la téléphonie numérique. Elles sont constituées de deux fils de cuivre, formant en général une paire torsadée. Equation de propagation dans le cas idéal. Un tronçon de longueur élémentaire, de longueur dx, peut être modélisé par le schéma suivant. A est l'inductance linéïque et G la capacité linéïque de la ligne. L = 250 nH m-1 ; G = 100 pF m-1. 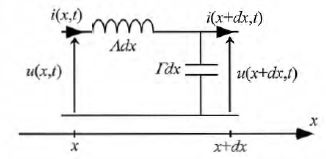Etablir les relations suivantes :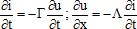 Loi des noeuds : i(x,t) = i(x+dx,t) + Gdx du(x+dx,t) /dt. i(x+dx,t) -i(x,t) = -Gdx du(x+dx,t) /dt. (i(x+dx,t) -i(x,t)) / dx = -G du(x+dx,t) /dt. Loi des mailles : u(x,t) = u(x+dx, t)+Ldx di(x,t)/dt. u(x+dx, t)-u(x,t) = -Ldx di(x,t)/dt. (u(x+dx, t)-u(x,t)) / dx = -L di(x,t)/dt. En déduire que la tension u vérifie une équation de propagation de d'Alembert et donner l'expression de la célérité c des ondes en fonction de A et G. Calculer c et commenter. 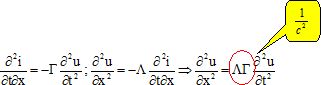c = (LG)-½ =(2,5 10-7*10-10)-½ =2,0 108 m/s. ( valeur égale à 0,66 fois la célérité de la lumière dans le vide ).   Prise en compte des faibles pertes. Afin de prendre en compte les dissipations d'énergie sous forme d'effet Joule le long de la ligne, on peut modifier le modèle en ajoutant une résistance en série avec la bobine. R représente la résistance linéïque de la ligne. 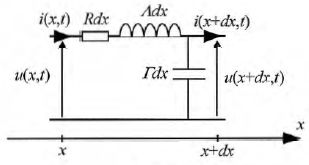On montre que la nouvelle équation de propagation de la tension est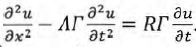 En cherchant une solution en notation complexe de la forme u = Um exp(j(wt-kx)), établir la relation de dispersion, reliant k à la pulsation w de la tension. 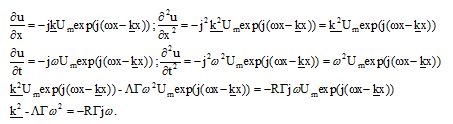Dans le cas des faibles pertes R <<Lw. Montrer que k=k'-jk" avec les expressions approchées suivantes : k' ~w/c et k"~R/(2Lc). 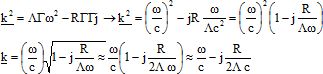On considère une portion de ligne de longueur L. Soit une onde de tension progressive se propageant dans le sens des x croissants. On note U0 son amplitude à l'entrée de la ligne et UL celle au bout de la distance L. Etablir la relation UL =U0 exp(-k"L).  En déduire l'atténuation en dB après un parcours d'une distance L en fonction de k" et L. u (0)= U0 exp(jwt) ; u (L)= Um exp(j(wt-kL))=U0 exp(jwt) exp(-jkL). UL = U0exp(-jkL)= U0exp(-jk'L+j2k"L) =U0exp(-jk'L)exp(-k"L). Identifier les parties réelles : UL =U0exp(-k"L) ln ( UL/U0) = -k"L ; 2,3 log( UL/U0) = -k"L ; log( UL/U0) = -k"L / 2,3. 10 log( UL/U0) = -10 k"L / 2,3. . Evaluation de l'atténuation. On cherche à justifier l'évolution de l'atténuation dans une ligne en fonction du diamètre a du fild e cuivre utilisé, telle qu'elle apparaît dans le tableau suivant, pour une fréquence donnée, égale à 1,1 MHz. Diamètre a du fil (mm) coefficient d'atténuation Att ( dB/km) 0,40 15 0,50 12,4 0,60 10,3 Le coefficient d'atténuation Att dans la ligne, exprimé en dB/m  peut s'écrire : Att = 10 R log (e) / (Lc) On rappelle que la résistance électrique d'un cylindre de résistivité r, de section S et de longueur L est r = rL/S. En régime sinusoïdal, la densité volumique de courant n'est pas uniforme dans un fil, en raison de l'effet de peau. On rappelle l'expression de l'épaisseur de peau, à une fréquence f, dans un milieu de résistivité r : d = (r/(pm0f))½. En admettant qu'en première approximation, le courant circule dans une épaisseur d<< a à la périphérie du fil, évaluer la section Sutile du fil effectivement parcourue par un courant en fonction du diamètre a et de l'épaisseur de peau d. Sutile = p/4(a2-(a-2d)2) = p/4(2d)(2a-2d) ~ p/4(2d)(2a)~pad. En déduire que la résistance linéïque effective de la ligne ( aller et retour ) peut s'écrire : R = 2/a (rm0f/p)½. pour un aller retour : R =2r/L =2 r/Sutile=2 r/(pad) =2 r(pm0f)½/(par½) =2/a (rm0f/p)½. Montrer que les valeurs du tableau ci-dessus sont cohérentes avec celles du coefficient d'atténuation linéïque en fonction du diamètre du fil. On donne r = 1,7 10-8 W m et µ0 = 4p 10-7 H m-1. (rm0f/p)½ = (1,7 10-8 *4p 10-7*1,1 106/p)½=8,65 10-5 ;  R =2/a (rm0f/p)½ = 1,73 10-4 / a W m-1. Att = 10 R log (e) / (Lc) =10 *1,73 10-4 / a  log(e) / (250 10-9 *2,0 108) =1,49 10-5 / a.(en dB/m) Att =1,49 10-2 / a dB/km pour un aller-retour. Att =7,45 10-3 / a dB/km pour un aller. Diamètre a (m) 4 10-4 5 10-5 6 10-5 Coefficient d'atténuation  pour un aller retour ( dB/km), valeur calculée. 18,6 14,9 12,4  . ..

menu