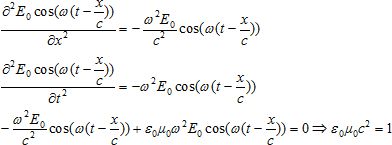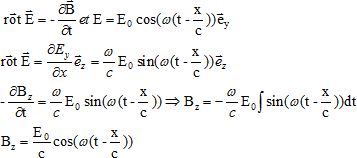|
|
|
|
Une
première façon d'approcher l'énergie qui nous vient du soleil est de
considérer qu'elle est transportée par des ondes électromagnétiques.
Considérons une onde électromagnétique sinusoïdale qui se propage dans
l'espace que l'on a répéré au moyen d'un repère cartésien R(0,x, y, z).
l'axe Ox étant colinéaire à la direction ST de la droite qui joint le
centre du soleil au centre de la terre. On assimile l'espace traversé
par l'onde au vide.
Le champ électrique de cette onde électromagnétique au point M(x, y, z ) du repère à l'instant t s'écrit :
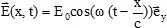 où w, c et E0 sont des constantes. où w, c et E0 sont des constantes.
Ce
champ est-il celui d'une onde progressive ou stationnaire ? Dans quelle
direction et quel sens se propage-t-il ? Quelle est l'unité de E0 ?
Le champ électrique d'une onde progressive se propage dans la même direction et le même sens que l'onde.
E0, amplitude du champ électrique, s'exprime en V m-1.
L'onde électromagnétique est constituée de deux champs, le champ
électrique et le champ magnétique. Maxwell a donné son nom à un système
de 4 équations qui relie le champ électromagnétique aux densité de
charge volumique r et densité de courant volumique 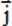 . .
Ecrire ces 4 équations. A quelle date les a-t-il proposées ? 1873.
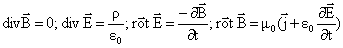 A
partir des équations de maxwel dans le vide, en absence de charges et
de courant, montrer que le champ électrique d'une onde
électromagnétique vérifie l'équation :
A
partir des équations de maxwel dans le vide, en absence de charges et
de courant, montrer que le champ électrique d'une onde
électromagnétique vérifie l'équation : 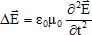 . .
div  = r
(nul s'il n'y ni charge, ni courant de conduction). = r
(nul s'il n'y ni charge, ni courant de conduction).
div B = 0 ;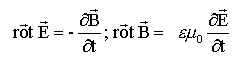
équation de propagation du champ
électrique :
Formons : 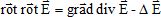 . .
Or div  =0 ( s'il
n'y ni charge, ni courant de conduction) =0 ( s'il
n'y ni charge, ni courant de conduction)
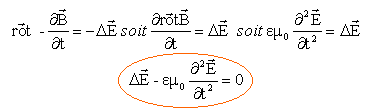 µ0c) µ0c)
En traduisant le fait que le champ électrique donné précédemment est solution de cette équation, établir le lien entre c, e0 et µ0.
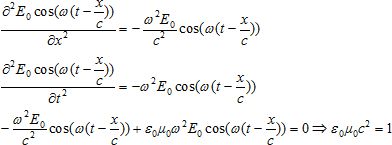
|
Décrire une expérience historique de mesure de c, en indiquant la date approximative à laquelle elle a été réalisée.
Fizeau en 1949 mesure la vitesse de la lumière à l'aide d'un dispositif à roues dentées.
La lumière passe à travers un miroir semi-réfléchissant puis à travers
une échancrure d'une roue dentée. Elle parcourt une distance D,
se réfléchit sur un miroir, revient vers la roue qui, entre-temps, a
tourné.
Connaissant D et de la vitesse de rotation de la roue ( telle que la
lumière réfléchie soit bloquée par une dent de la roue ) on peut
déterminer la vitesse de la lumière.
La valeur de c a été fixée à 299 792 458 m/s par le bureau internationnal des poids et mesures.
Quelle conséquence cela a-t-il eu sur la définition du mètre ?
Cette valeur a permis de définir du mètre : distance parcourue par la lumière dans le vide en 1 /299 792 458 seconde.
Déterminer l'expression du champ magnétique en M à l'instant t.
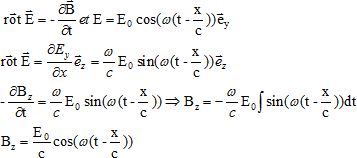
Préciser l'unité du champ magnétique. Le tesla (T).
Les ondes électromagnétiques émises par le soleil transportent de l'énergie. Considérons une surface S dont la normale est orientée selon le vecteur ex.
Pour calculer l'énergie qui traverse cette surface pendant une durée dt, on peut utiliser le vecteur de Poynting.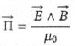
Exprimer l'unité du vecteur de Poynting en fonction des unités watt et mètre.
Une puissance par unité de surface s'exprime en W m-2.
Calculer le vecteur de Poynting pour l'onde envisagée, en un point M(x, y, z). Commenter la direction de ce vecteur.
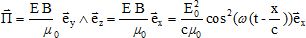
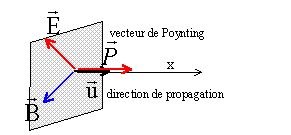
L'énergie
se propage dans le sens de l'onde à la vitesse c.
En déduire la valeur moyenne temporelle du vecteur de Poynting.
La valeur moyenne du terme en cos2 vaut ½ ; la valeur moyenne du vecteur de Poynting vaut donc : E02 / (2µ0c).
La puissance moyenne rayonnée par le soleil est telle qu'au niveau de
la surface de la terre la puissance reçue par unité de surface
est P =1000 W m-2. µ0 = 4 p 10-7 SI.
En déduire la valeur de E0.
P = E02 / (2µ0c) ; E0 = (2 Pµ0c)½ =(2000 *4*3,14 10-7 *3,0 108)½ =8,7 102 V m-1.
Une
seconde façon d'aborder l'énergie qui nous vient du soleil est de la
considérer comme une somme des quanta d'énergie transportés par les
photons qui la constituent.
Dans le cas de la photographie numérique, détermination du nombre de photons par pixel nécessaires à la réalisation d'une photographie de qualité.
La puissance moyenne rayonnée par le soleil est telle qu'au niveau de
la surface de la terre la puissance reçue par unité de surface
est P =1000 W m-2.
Les objets éclairés renvoient dans toutes les directions la lumière
solaire. Le flux de photons nous parvenant de ces objets vaut un
centième du flux solaire, soit 10 Wm-2.
Taille du capteur CCD de l'appareil photo : 18 x13,5 mm2. S = 18*13,5 = 243 mm2 = 2,43 10-4 m2.
Puissance reçue par le capteur :10 * 2,43 10-4 = 2,43 10-3 W.
La vitesse d'obturation varie de 60 à 1/4000 s.
Energie recue par le capteur dans le cas de la plus petite vitesse d'obturation : 2,43 10-3 / 4000 =6,075 10-7 ~6,1 10-7 J.
Energie moyenne d'un photon du spectre visible : E = h c / l = 6,63 10-34 *3 108 / (600 10-9) =3,3 10-19 J.
Nombre moyen de photons reçus par le capteur : 6,1 10-7 / 3,3 10-19 ~2 1012.
Nombre de pixels du capteur : 12 millions.
Nombre moyen de photons arrivant sur chaque pixel : 2 1012 / (12 106) =1,5 105.
Pour une image de qualité, 10000 photons doivent arriver sur un pixel.
|
|

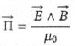
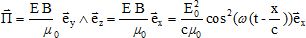
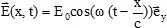 où
où 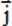 .
.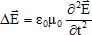 .
.
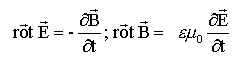
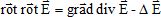
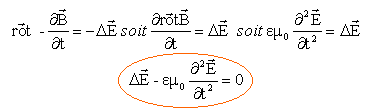 µ0c)
µ0c)