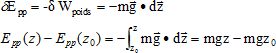|
|
|
|
Soit
un objet de masse m, assimilé à un point, soumis à un ensemble de
forces dont la résultante est notée F. On étudie l'évolution de ce
point dans un référentiel galiléen R0 et on note v la vitesse dans le référentiel étudié.
Commençons par établir l'expression de l'énergie cinétique, dans le cadre de la mécanique classique..
Définir la notion de référentiel galiléen. Donner un exemple de référentiel galiléen et un exemple de référentiel non galiléen.
Un référentiel est un solide par rapport auquel
on étudie un mouvement. On prend souvent comme référentiel le solide
Terre.
Référentiel galiléen : dans ce référentiel le principe
d'inertie ou 1ère loi de Newton s'applique " un point matériel
pseudo-isolé demeure dans son état de repos ou de mouvement rectiligne
uniforme".
Le référentiel héliocentrique a pour origine le Soleil et des axes
pointant vers des étoiles lointaines qui paraissent fixes.
Le référentiel géocentrique a pour origine le centre de la Terre et
des axes parallèles à ceux du référentiel héliocentrique. Ce référentiel peut
être considéré comme galiléen pour des durées de quelques minutes. ( La Terre
effectue un mouvement de rotation autour d'un axe nord sud)
Un
véhicule accélérant ou ralentissant ne constitue pas un référentiel
galiléen : il n'est pas animé d'un mouvement rectiligne uniforme par
rapport au référentiel terrestre.
Galilée a formulé le principe de relativité galiléenne.
A quelle époque Galilée a-t-il vécu ? Enoncer une formulation actuelle de ce principe.
Galilé ( 1564 -1642 ). Les lois de la physiques sont identiques pour tous les référentiels inertiels ( galiléens ).
Etablir et énoncer le théorème de l'énergie cinétique.
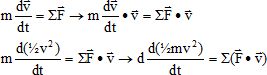
La variation de l'énergie cinétique d'un système (S) entre deux dates
t1 et t2 est égale à la somme des travaux des forces
appliquées au système durant des deux dates .
Le point matériel est ici considéré dans le champ de pesanteur uniforme 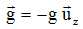 avec uz le vecteur unitaire de l'axe vertical orienté vers le haut. avec uz le vecteur unitaire de l'axe vertical orienté vers le haut.
Etablir l'expression de l'énergie potentielle de pesanteur du point matériel.
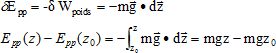
Pourquoi dit-on que le poids est une force conservative ?
Une force est dite conservative lorsque son travail est indépendant du chemin suivi par son point d'action.
Proposer une solution succincte à l'exercice de mécanique ci-dessous.
Looping dans un parc d'attraction.
En 2009, un parc d'attraction s'est doté d'un nouveau grand huit à fortes sensations. On peut lire sur le descriptif :
" Top départ, c'est parti.... de 0 à 100 km/h en 2,5 secondes chrono !
Un
démarrage par catapulte propulse le visiteur à 40 mde haut, un instant
de pur adrénaline ! S'enchaîne un looping à une hauteur de 40 m,
sensation nouvelle pour le visiteur ...qui se retrouve avec la tête à
l'envers.
Estimer la valeur numérique de l'accélération du wagon pendant la phase de catapultage. Comparer à g = 9,81 m s-2.
a = Dv / Dt avec vfinale = 100 /3,6 = 27,8 m/s.
a = (27,8-0) / 2,5 =11,1 m s-2, du même ordre de grandeur que g.
|
.
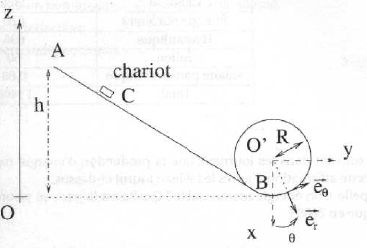
Le looping simplifié est constitué d'une
gouttière de lancement dont le point le plus haut est situé à une
hauteur h au dessus du sol et permet de guider un chariot vers un rail
circulaire de rayon R. Il ne comporte donc pas de phase de catapultage,
mais cela est compensé par un point de départ plus élevé du chariot. De
plus la liaison entre le chariot et le rail est unilatérale ( elle
interdit le rapprochement de deux corps au delà du contact, mais
n'interdit pas leur éloignement ). Le chariot et ses occupants ont une
masse m = 10 tonnes. L'ensemble du chariot et de ses occupants est
assimilé à un point matériel C. L'étude du mouvement est réalisée dans
le référentiel terrestre R0 supposé galiléen.
Dans un premier temps, le modèle adopté pour la liaison entre le rail
et les roues du chariot est celui de la liaison parfaite, c'est à dire
qui ne dissipe pas d'énergie. De plus les frottements de l'air sur le
chariot et les passagers est négligée. Le chariot est immobile en A.
Quelle forme d'énergie possède-t-il ?
L'énergie mécanique du système est sous forme potentielle de pesanteur.
Le chariot est abandonné sans vitesse initiale au point A.
Exprimer sa vitesse lorsqu'il arrive en B.
Le système est soumis à son poids et à l'action du support,
perpendiculaire au support. En conséquence, cette dernière force ne
travaille pas.
Th de l'énergie cinétique entre A et B : ½mvB2 -0 = mgh ; vB= (2gh)½.
Pour la seconde partie du mouvement, à partir de B, le chariot est repéré par ses coordonnées polaires R et q.
Justifier que la force que le rail circulaire exerce sur le chariot puisse s'écrire 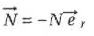 et représenter les différentes forces qui agissent sur le chariot. et représenter les différentes forces qui agissent sur le chariot.
La liaison chariot-rails étant parfaite, l'action des rails sur le
charriot est perpendiculaire au rail. Les rails guident le chariot et
exerce une action dirigée vers O'.
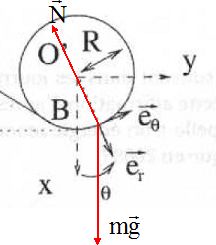
Etablir l'expression de N en fonction de q : N = mg((3 cos q) + 2(h/R-1)).
La seconde loi de Newton s'écrit suivant er : -N + mg cos q = -mv2/R. (1)
Théorème de l'énergie cinétique entre B et la position repérée par q :
½mv2 - ½mvB2 =½mv2 - ½m 2gh = -mgR(1-cos q) ; v2 = 2gh-2gR(1-cos q) = 2g(h-R+Rcos q). Repport dans (1)
N = mg cos q +2mg( h-R+Rcos q)/ R = mg cos q + 2mg( h/R-1+cos q) ;
N = mg ((3 cos q) + 2(h/R-1)).
Etablir une condition sur h/R pour que le looping soit éffectué.
Le chariot doit rester au contact des rails : N >0 quelle que soit la valeur de q, en particulier lorsque q = p.
3 cos p + 2(h/R-1) >0 ; -3+ 2(h/R-1) >0 ; h/R-1> 1,5 ; h / R > 2,5.
Désormais
les hypothèses d'absence de frottement de l'air et de la liaison
parfaite sont abandonnées. La mise en équation est plus difficile.
Une simulation numérique, à l'aide de la méthode d'Euler, permet
d'obtenir les courbes suivantes : évolution au cours du temps de
l'énergie cinétique Ec, de l'énergie potentielle Ep, de l'énergie totale EM
et de la réaction normale du plan. L'origine de l'énergie potentielle
est prise au point le plus bas du looping. A l'instant t=0, on
abandonne le chariot au point A sans vitesse initiale.
Pour quels travaux relevant du domaine de la physique connaissez-vous Euler ? A quelle époque a-t-il vécu ?
Euler ( 1707 - 1783 ) ; travaux en mécanique des fluides, astronomie.
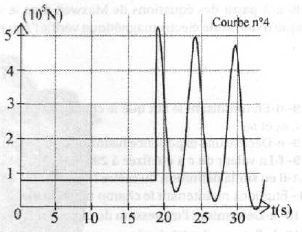
Associer à chaque courbe la grandeur associée en justifiant.
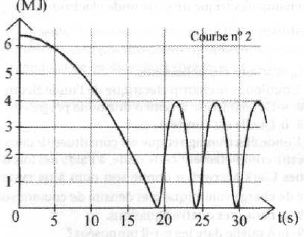
Energie potentielle : maximale à t = 0, constante au sommet du looping , nulle en B.
|
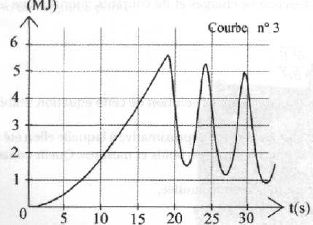
Energie cinétique : nulle à t=0, minimale au sommet du looping et maximale en B
|
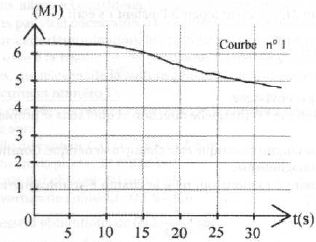
Energie mécanique, somme des énergies potentielle et cinétique, décroissante au cours du temps du fait des frottements.
|
Action du plan, constante entre A et B, minimale au sommet du looping, discontinue au premier passage en B.
|
Estimer la hauteur initiale et la vitesse maximale atteinte.
L'énergie potentielle est maximale à t=0 et vaut environ 6,4 106 J ; hmax = 6,4 106 / (mg) = 6,4 106 / ( 104 *9,81) ~ 65 m.
En bas du plan, vmax = (2gh)½ =(2*9,81*65)½ ~ 36 m/s.
Au sommet du looping, l'énergie potentielle vaut 4 106 J ; 2R = 4 106 / (mg) = 4 106 / ( 104 *9,81) ~ 40 m.
h/R = 65/20 = 3,2. La condition de réussite du looping h / R > 2,5 est bien vérifiée.
A quelle date le mobile quittera-t-il la gouttière ? Combien de tours complets a effectué le chariot dans cette simulation ?
Le mobile quitte la gouttière dès que l'action du plan devient nulle : t ~33 s ( graphe 4 ). Il a effectué trois tours complets.
Que
se passe-t-il au moment où le mobile passe de la rampe de lancement au
rail du looping ? Que faudrait-il faire pour améliorer la simulation ?
On observe une discontuinité de l'action du plan.
|
|

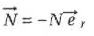 et représenter les différentes forces qui agissent sur le chariot.
et représenter les différentes forces qui agissent sur le chariot.
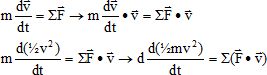
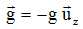 avec uz le vecteur unitaire de l'axe vertical orienté vers le haut.
avec uz le vecteur unitaire de l'axe vertical orienté vers le haut.