Cinétique enzymatique de dénitrification bactérienne dans les sols : Capes physique chimie 2013. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. . La population microbienne impliquée et son activité respiratoire sont supposées constantes, ce qui conduit à un nombre constant d'électrons produits par unité de temps par les bactéries réductrices des composés azotés. La réduction du dioxygène s'appuyant sur  des populations plus diverses, elle met en jeu un nombre d'électrons disponibles par unité de temps plus grand que celui qui concerne la réduction des espèces azotées La concurence entre les accepteurs d'électrons est caractérisée par leur concentration respective, ainsi que par leur affinité pour les électrons. L'effet inhibiteur du dioxygène sur le processus de dénitrification s'explique par sa très grande affinité pour la réduction enzymatique : tant que le dioxygène est présent, les réductions des composés azotés sont trop lentes pour être observées. Les  équations des réactions de réduction successives mises en oeuvre sont décrites ci-après, les électrons étant fournis à vitesse constante par l'activité bactérienne : O2 +4H++4e- = 2H2O NO3-+2H++2e- = NO2- + H2O 2NO2- +6H++4e- = N2O +3H2O N2O +2H++2e- = N2 + H2O Ces réductions se font en présence d'enzymes spécifiques à chaque espèce chimique et on admet les mécanismes suivants pour ces catalyses enzymatiques : 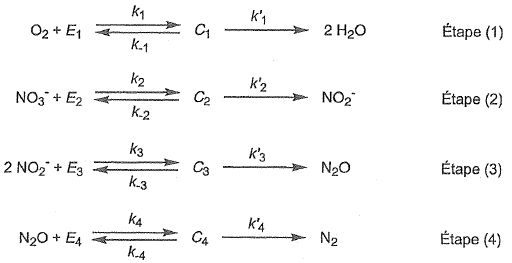Les Ei ( avec i = 1, 2, 3 ou 4) sont des enzymes spécifiques à chaque espèce chimique et Ci ( avec i =1, 2, 3 ou 4) sont des complexes enzyme-substrat formés respectivement à partir de O2, NO3-, NO2- et N2O. Les ki, k-i et k'i sont des constantes de vitesse. Chaque espèce chimique X intervient dans le mécanisme par sa concentration molaire notée [X]. 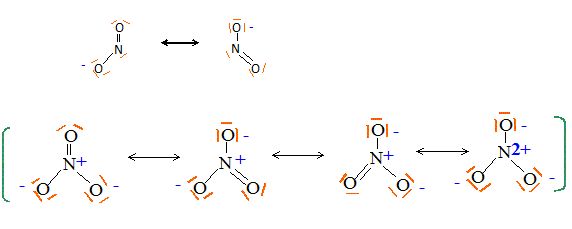Ecrire les formules de Lewis des ions NO3-, NO2- et de la molécule N2O.   . Exprimer vdisp(O2), vitesse totale de disparition du dioxygène en fonction des concentrations et constantes de vitesse nécessaires. L'étape 1 est un équilibre qui s'établit rapidement ; l'étape 2 est lente, c'est donc elle qui impose la vitesse. La vitesse de la réaction est égale à : v ~k'1[C1] ;  vdisp(O2) ~ k'1[C1]. On admet que l'on peut appliquer l'approximation des états stationnaires aux complexes enzyme-substrat. Exprimer la concentration du complexe C1 en fonction des concentrations en E1 et en O2 et des constantes de vitesses adéquates. d[C1]/dt = 0 = k1 [O2][E1]-k-1[C1]-k'1[C1] [C1] = k1 [O2][E1] / (k-1+k'1).  (1). En utilisant l'équation de conservation de l'enzyme, montrer que : [C1] = [O2][E1]0 / (KM1 +[O2]). [E1]0 désigne la concentration totale en enzyme sous toutes ses formes et KM1 une constante qu'on exprimera en fonction des constantes de vitesses adéquates. [E1]0 = [E1] +[C1] ; [E1] = [E1]0 -[C1], repport dans (1). (k-1+k'1) [C1] = k1 [O2]([E1]0 -[C1]). (k-1+k'1+ k1 [O2] ) [C1] =  k1 [O2][E1]0 ; ((k-1+k'1) / k1  +[O2] ) [C1] =   [O2][E1]0 ; [C1] =   [O2][E1]0 / ((k-1+k'1) / k1  +[O2] ). KM1 =(k-1+k'1) / k1. En déduire l'expression de vdisp(O2). vdisp(O2) = k'1 [O2][E1]0 / (KM1 +[O2]). De la même façon, exprimer les vitesses vdisp(NO3-), vdisp(NO2-) et vdisp(N2O), respectivement vitesses de disparition de NO3-, NO2- et de N2O. On remarquera que des espèces sont formées par une étape et consommées par une autre. vdisp(NO3-) = v formation (NO2-) = k'2[C2]= k'2 [NO3-][E2]0 / (KM2 +[NO3-]). vdisp(N2O) = k'4[C4] =k'4 [N2O][E4]0 / (KM4 +[N2O]). Vitesse de la réaction 3 : v3 = k'3[C3]= k'3 [NO2-][E3]0 / (KM3 +[NO2-]) ;  vdisp(NO2-)= 2 v3 - v formation (NO2-). vdisp(NO2-) =2 k'3 [NO2-][E3]0 / (KM3 +[NO2-])- k'2 [NO3-][E2]0 / (KM2 +[NO3-]). On constate expérimentalement  que les courbes représentant l'évolution des concentration des différentes espèces réduites sont assimilables à des segments de droites. Quelle approximation peut-on effectuer dans l'expression de la vitesse vdisp(O2) pour rendre compte de ces résultats expérimentaux ? vdisp(O2) = -d [O2] /dt = constante ;  si KM1 << [O2] alors k'1 [O2][E1]0 / (KM1 +[O2])~ k'1 [E1]0. Dans le cadre de cette approximation, l'enzyme est dite saturée. Que signifie cette affirmation ? Toutes les molécules d'enzyme sont complexées avec leur substrat spécifique. La vitesse maximale est atteinte. Il a été constaté expérimentalement que le dioxygène inhibe la réduction des ions nitrate et que les ions nitrate et nitrite inhibent  celle de l'oxyde nitreux. En d'autres termes, la réduction des ions nitrate ne commence que lorsque le dioxygène a disparu presque totalement et la réduction de N2O ne commence que  lorsqu'il n'y a pratiquement plus d'ions nitrate ni d'ions nitrite. Par ailleurs la concentration en ion nitrite reste très faible et très inférieure aux autres concentration pendant tout le processus de dénitrification. Les conditions sont telles que la production d'électrons par les bactéries est le facteur limitant des réductions des composés azotés. 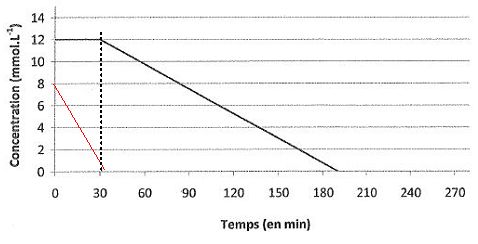Pour des concentrations initiales e [O2]0 = 8,0 mmol/L et [NO3-]0 = 12,0 mmol/L, on donne ci-dessous la courbe représentative de l'évolution de la concentration en ion nitrate en fonction du temps. Tracer sur le graphe la courbe donnant l'évolution de la concentration en dioxygène en fonction du temps dans les conditions mentionnées ci-dessus. ( voir courbe rouge ). 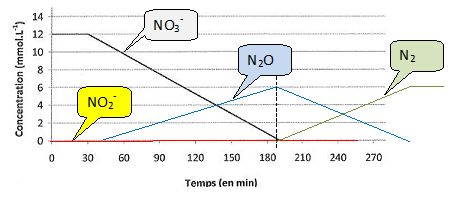Dans l'hypothèse d'un débit constant en électrons produits par les bactéries réductrices des espèces azotées, en tenant compte du nombre d'électrons échangés lors des réductions successives des composés azotés, tracer sur le même graphe les autres courbes représentant les évolutions temporelles des concentrations [NO2-], [N2O] et [N2]. Les valeurs absolues despentes des segments de droite sont proportionnelles aux nombre d'électrons échangés. .

menu