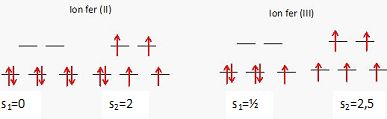|
|
|
|
Les
ions fer (II) et fer (III) s'entourent de six ligands dans un
environnement octaèdrique. Cet environnement conduit à une levée de
dégénérescence des niveaux 3d du fait d'interactions différentes entre
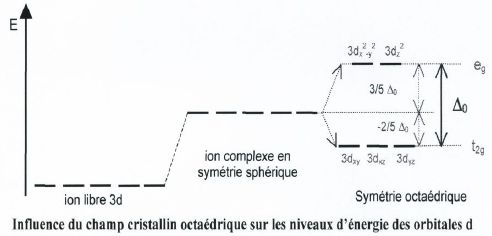
les différents types d'orbitales 3d et des ligands. D0 représente l'éclatement du champ cristallin octaèdrique, c'est à dire la différence énergétique entre le niveau eg et le niveau t2g.
Le schéma suivant représente le diagramme d'énergie des orbitales 3d
avant et après la levée de dégénérescence dans le champ cristallin.
Donner le nombre n d'électrons dans la couche 3d des ions fer(II) et fer (III).
Configuration électronique de l’atome de fer ( Z=26) dans son état
fondamental : 1s2 2s2 2p6 3s2
3p6 3d6 4s2.
Nature des ions les plus courants de cet élément : Fe2+ 1s2
2s2 2p6 3s2 3p6 3d6
( perte facile des 2 électrons 4s2)
et Fe3+ 1s2 2s2 2p6 3s2
3p6 3d5 ( la couche 3d5 est à moitié
pleine).
Deux états, dits "bas spin" (BS) et "haut spin" (HS) sont possibles.
Pour chacun des deux ions, représenter les diagrammes d'énergie HS et BS, en déduire les valeurs s1 et s2 du nombre de spin total de chaque état et leur attribuer les qualiquatifs diamagnétique ou paramagnétique.
Un ligand à champ fort est
un ligand pour lequel l'éclatement
D0
du champ cristallin est supérieur à
l'énergie d'appariement P : le maximum d'électrons sont
appariés et le spin est faible.
Un ligand à champ faible est
un ligand pour lequel l'éclatement
D0
du champ cristallin est inférieur à
l'énergie d'appariement P : le maximum d'électrons sont
célibataires et le spin est fort.
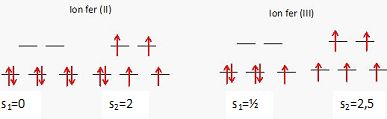
Un composé est diamagnétique si tous les électrons sont appariès. Un composé est paramagnétique s'il possède un ou des électrons non appariès.
La grandeur notée P représente l'énergie de répulsion de deux électrons placés dans une même orbitale 3d.
Pour chacun des deux ions complexes, exprimer en fonction de D0 et P, la différence d'énergie DE = E(HS)-E(BS) entre les deux états HS et BS. Conclure.
Ion fer (II) : bas spin : DE = 6(-2/5 D0) + 3P.
Haut spin : DE = 4(-2/5 D0) +2(3/5 D0)+ P = -2/5 D0 + P.
Ion fer (III) : bas spin : DE = 5(-2/5 D0) + 2P.
Haut spin : DE = 3(-2/5 D0) +2(3/5 D0) = 0.
La configuration la plus faible en énergie est la plus stable.
A quelle condition sur P et D0, l'état électronique BS du complexe du fer (II) est-il le plus stable ?
6(-2/5 D0) + 3P <- 2/5 D0 + P soit P < D0.
|
En
modifiant l'environnement chimique d'un ion fer (II), une transition
entre les deux états électroniques BS et HS est susceptible
d'intervenir. Dans la suite du problème, on considère des ions fer (II)
complexés par 3 ligands bidentates..
Que signifie "bidentate" ? Illustrer le propos en prenant comme exemple l'éthylène diamine notée (en).
Les ligands bidentates sont des ligands pouvant se lier à un ion métallique avec deux de leurs atomes, comme l'éthylènediamine.
1,2-diaminoéthane H2NCH2-CH2NH2 : les deux doublets libres des deux atomes d'azote peuvent établir deux liaisons
de coordination avec l'ion fer (II).
Faire un schéma de l'ion complexe [fe(en)3]2+ et montrer qu'il existe sous la forme de deux énantiomères.
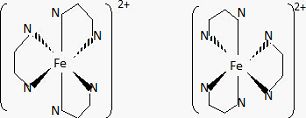
Ce complexe ne possède aucun élément de symétrie, il existe donc sous forme de deux énantiomères.
Citer une technique expérimentale qui permettrait de distinguer ces deux énantiomères.
Dédoublement du mélange racémique par formation de diastéréoisomères
suivie d'une cristallisation ou d'une chromatographie avec phase
stationnaire chirale.
La dispersion optique rotatoire (DOR) et le dichroïsme circulaire (DC)
(effet Cotton ) permettent de distinguer ces deux énantiomères.
|
A
l'état solide, chaque ion complexe peut se trouver soit dans l'état BS,
soit dans l'état HS. L'équation de la réaction de transition entre ces
deux états s'écrit : BS = HS. Une solution solide comporte donc un
mélange d'ions complexes BS et HS à l'équilibre.
On rappelle que s1 et s2 désignent les valeurs du
nombre de spin total respectivement dans les états BS et HS. Par
analogie avec la quantification du moment orbital dans l'atome, indiquer le nombre de projections possibles pour un spin total s1 ou s2. On notera W1 et W2 ces valeurs respectivement pour s1 et s2.
W1 = 2 s1+1 = 1 ; W2 = 2 s2+1 = 5.
En thermodynamique statistique, on montre que l'entropie S s'écrit S = R ln W.
Montrer
que le changement de spin lors de la transition de l'état BS vers
l'état HS s'accompagne d'une contribution à la variation d'entropie de
réaction DrS° = R ln 5 et déterminer numériquement sa valeur
DrS° = R ln W2 - Rln W1 = R ln( W2 / W1) = Rln 5 = 8,314 ln 5 = 13,4 J mol-1K-1.
A
pression constante, les fractions molaires des ions complexes dans
l'état BS et dans l'état HS peuvent-elles être déterminées si on fixe
la température ? Justifier.
Un seul constituant indépendant ; solution solide : une seule phase ; à pression constante, la variance est égale à 1.
Si on fixe la température, la composition du système est déterminée.
Synthétisé au milieu des années 1960, le complexe Fe(phen)3(SCN)2
est l'un des premiers complexes qui a permis la transition HS=BS. La
figure suivante donne la variation de la fraction molaire xHS des ions complexes dans l'état HS en fonction de la température T. Les points expérimentaux sont indiqués par des cercles.
Déterminer gphiquement la température T½ pour laquelle le nombre de complexes dans l'état BS est égal au nombre de complexes dans l'état HS.
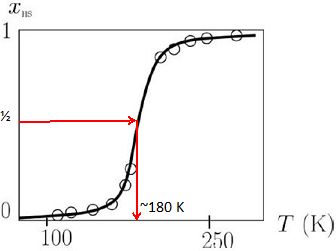
|
L'enthalpie standard de la réaction de transition HS=BS à la température T½ vaut DrH°=8,75 kJ mol-1.
Déterminer l'entropie standard DrS° expérimentale de la réaction de transition BS=HS à la température T½.
HS=BS ; constante d'équilibre à T½ K = [HS] / [BS] = 1 ; DrG° = -RT ln K = 0.
DrG° =DrH°-T½ DrS° expérimentale = 0 ; DrS° expérimentale =DrH° / T½ =8,75 103 / 180 = 48,6 J mol-1 K-1.
On signale une augmentation des longueurs de liaison Fe-N lors de la transition de l'état BS vers l'état HS.
Justifier que DrS° expérimentale soit supérieure à DrS°.
Dans l'état BS, les électrons peuplent majoritairement les niveaux liants t2g.
La molécule dans l’état HS possède des distances Fe-N qui sont
plus importantes que dans l’état BS ( peuplement partiel des orbitales
anti-liantes eg).
La différence d'entropie est attribuée à l’entropie vibrationnelle : le
mode d’élongation de la distance Fe-N ainsi que les modes de distorsion
de l’octaèdre Fe(phen)3(SCN)2.
|
|