|
|
L'iode 123.
L'iode 123 12353I peut se produire à partir du
bombardement d'un noyau d'antimoine 121 12151Sb
par une particule alpha.
Ecrire l'équation de
cette réaction nucléaire.
12151Sb
+ 42He
---> 12353I
+ 210n.
Rappeler le nombre
maximal d'électrons que chaque sous couche s, p, d, f peut contenir.
s : 2 électrons au plus ; p : 6 électrons au plus ; d : 10 électrons au
plus ; f : 14 électrons au plus.
Donner
la configuration électronique d'un atome d'iode dans son état
fondamental après avoir rappelé le moyen utyilisé pour retrouver
l'ordre croissant de remplissage des différentes sous couches.
Règle de Klechkowski : les sous couches sont remplies de sorte que n+l soit croissant.
1s2 2s2 2p6 3s2 3p6
4s2 3d10 4 p6 5s2 4 d10
5p5.
En
déduire la position de l'élément iode dans la classification périodique.
17ème colonne, 5ème ligne.
Désintégration.
L'iode 123 dont la période ou demi-vie vaut t½ = 13,2 h se
désintègre par capture électronique pour former un noyau Y. On observe
alors un rayonnement gamma d'énergie 159 keV et des rayons X d'énergie
27,47 keV et 30,99 keV.
Ecrire
l'équation de la réaction correspondant à la capture électronique.
Capture électronique : 11p + 0-1 e = 10n + neutrino ; Z diminue de
1 et N augmente de 1.
12353I
+ 0-1 e ---> 12352Te*
+ neutrino suivie de 12352Te*
---> 12352Te
+ gamma (
désexcitation du noyau de tellure ).
Expliquer
les valeurs d'énergie des photons X produits.
On donne les énergies de liaisons des électrons du tellure :
EK =31,81 keV ; EL =4,34 keV ; EM
=0,82 keV.
Après
la capture électronique, le noyau n'est pas totalement stable et reste
excité. De plus l'électron absorbé, le plus souvent un de la couche K,
laisse un ''trou'' qui nécessite alors un réarrangement du cortège
électronique.
Transition L vers K : EK -EL =
31,81-4,34 =27,47 keV.
Transition M vers K
: EK -EM =
31,81-0,82 =30,99 keV.
Montrer
que la constante radioactive de l'iode 123 est égale à 1,46 10-5
s-1.
l = ln2 / t½
= ln2 / (13,2*3600) =1,46 10-5 s-1.
L'iode 123 est utilisé pour effectuer des scintigraphies thyroïdiennes.
Deux heures avant l'examen on injecte par voie intraveineuse, une dose
d'iode 123 qui présente une activité Ainj
= 7,0 Mbq. Cet iode radioactif est métabolisé par la thyroïde de la
même façon que l'isotope stable, l'iode 127. L'examen consiste d'abord
a explorer la thyroïde par une caméra à scintillations qui localise et
mesure le rayonnement gamma émis par l'iode radioactif. La caméra,
associée à un ordinateur permet de visualiser l'activité métabolique de
la glande.
Calculer
le nombre de noyaux radioactifs d'iode 123 injectés dans le patient.
A = l N; N = A/ l = 7,0 106 / (1,46 10-5) =4,8 1011.
L'iode 123 se répartit à x% dans la thyroïde et à y % dans l'organisme
hors thyroïde. Cette dernière partie est évacuée principalement par
voie rénale. On ne considèrera ici que l'activité liée aux
désintégrations dans la thyroïde.
On mesure au début de l'examen une activité de la thyroïde qui vaut A =
1,4 MBq.
Que
vaut à cet instant le taux de captation x ?
Activité de l'iode 123 dans l'organisme au bout de deux heures.
A(t=2) = A0 exp (-lt)
= 7,0 exp(-1,46 10-5 *2*3600) =6,3 MBq.
x = 1,4 / 6,3 =0,22 ( 22 %).
Calculer
la durée en heure et en minute, pour laquelle l'activité de la thyroïde
est passée de 1,4 MBq à 0,28 Mbq.
0,28 = 1,4 exp(-1,46 10-5 t) ; ln(1,4 / 0,28) = 1,46
10-5 t ; t = 1,1 105 s ou
30,6 h soit 30 h 37 min.
Cet examen entraîne au final une dose absorbée par la thyroïde de
490mGy.
Calculer
la dose équivalente et la dose efficace reçue par la thyroïde.
Dose équivalente en sievert = dose absorbée en gray fois un
facteur de pondération. Ce facteur vaut 1 pour les rayons gamma.
Dose équivalente = 0,490 *1 = 0,490 Sv.
Dose efficace ( Sv) = dose équivalente fois un facteur de
sensibilité de l'organe ( 0,04 pour la thyroïde ).
Dose équivalente : 0,490*0,04 =0,0196 ~0,020 Sv.
|
| .
. |
.
|
Iode
131.
Sa période ou demi-vie vaut t½ =28,04 jours.
Ecrire
l'équation de la réaction de désintégration d'un noyau d'iode 131. De
quel type de radioactivité s'agit-il ?
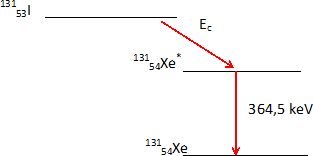
13153I ---> 13154Xe
+0-1e. Radioactivité de type ß-.
Calculer
la perte de masse puis l'énergie libérée par la désintégration d'un
noyau d'iode 131.
m(13153I) =130,877053 u ; m(13154Xe) = 130,875462 u ; m(0-1e) = 5,486 10-4 u. 1 u = 931,5 MeV c-2.
Dm = m(13154Xe) +m(0-1e) -m(13153I) =130,875462 +5,486 10-4 -130,877053
= -1,0424 10-3 u.
Energie libérée : -1,0424 10-3
*931,5 = -0,971 MeV = -971 keV
Comment se partage
l'énergie libérée ?
L'énergie libérée
se partage entre l'électron émis ( énergie cinétique) le neutrino et le
photon gamma. L'énergie cinétique du noyau de Xenon est négligeable.
Déterminer en keV,
l'énergie cinétique maximale de la particule chargée émise.
Le noyau d'iode 131 est initialement au repos.
971 -364,5 =606,5 keV.
Radio-iodothérapie.
Dans le cas de certains traitements, on utilise l'iode 131 pour
détruire les cellules cancereuses situées dans la thyroïde. On demande
au patient d'avaler une gelule contenant de l'iode 131 ayant une
activité A0 =900 MBq. Celui-ci sera en chambre radioprotégée
pendant deux jours. Un document remis à la sortie demande pendant 8
jours après la sortie :
d'éviter le contact avec des enfants de moins de 15 ans et des femmes
enceintes
de dormir à distance du conjoint.
L'énergie moyenne des particules chargées émises par les noyaux d'iode
131 vaut Emoy =0,191 MeV.
Le parcours moyen dans la thyroïde de ces particules vaut R = 0,50 mm.
L'énergie moyenne par ionisation ( ou paire ion / électron ) vaut w = 33 eV.
Calculer
le nombre total d'ionisations créées par une particule chargée.
Emoy / w = 0,191
106 / 33 = 5,79 103.
Calculer
la DLI ( densité linéïque d'ionisation ) de cette particule chargée.
Nombre de paires
électrons / ions par unité de longueur :
DLI
= 5,79
103 / (5 10-4)
=1,16 107 ion m-1 ou 11,6 ion µm-1.
La gélule est présentée dans un flacon en verre, lui même placé dans un
pot en plomb d'épaisseur e = 2,5 cm. La CDA, couche de demi-atténuation
pour les photons gamma d'énergie 364,5 keV vaut 3,00 mm dans le plomb.
On néglige l'atténuation par le verre.
Calculer
le pourcentage de photons gamma sortant du pot.
Coefficient d'atténuation linéïque du plomb : µ = ln2 / CDA = ln2 /3,00
=0,231 mm-1.
I / I0 =exp(-µe) = exp(-0,231*25) =3,1 10-3 (
0,31 %).
Globalement, 75 % de l'activité de l'iode 131 administrée est éliminée
dans l'urine dans un délai de 48 heures.
Justifier
les conseils remis à la sortie du patient.
Activité résiduelle de l'iode 131 à sa sortie : 900*0,25 =225 MBq.
Activité au bout de 8 jours : A = 225 exp(-lt) avec l = ln2 / t½ =ln2 /
28,04 =2,44 10-2 j-1.
A = 225 esp(-2,44 10-2 *8 )=185 Bq.
Activité moyenne durant ces 8 jours : ~200 MBq.
Activité résiduelle 2 jours après la sortie : 200 *0,25 =50 Mbq.
Activité
résiduelle 4 jours après la sortie : 50 *0,25 =12,5 Mbq.
Activité
résiduelle 6 jours après la sortie : 12,5 *0,25 =3,1 Mbq.
Activité
résiduelle 8 jours après la sortie : 3,1 *0,25 =0,8 Mbq.
|
|
|
Tchernobyl.
La présence d'iode 131, expulsé dans l'air au cours de cet accident nucléaire, peut s'expliquer par la réaction suivante :
23592U +10n--->13153I +10239Y +...
Compléter l'équation. De quel type de transformation nucléaire s'agit-il ?
Conservation de la charge : 92 =53+39+x ; x = 0.
Conservation du nombre de nucléons : 235+1 =131+102+y ; y =3.
23592U +10n--->13153I +10239Y +310n.
Réaction de fission de l'uranium provoquée par un neutron ( réaction en chaîne ).
De l'iode 131 avec une activité totale estimée à 1,2 1018 Bq s'est retrouvée dans l'atmosphère suite à cet accident.
Une personne habitant dans la zone des trente kilomètres de la centrale
a absorbé au niveau de la thyroïde une dose D = 1,4 Gy. La thyroïde de
cette personne a une masse M = 20 g.
Calculer la quantité d'énergie reçue par cette thyroïde.
E = D M = 1,4 *0,020 = 2,8 10-2 J.
On peut estimer l'activité initiale reçue A par la thyroïde au cours de cet accident : A(MBq) = 23,4 D(Gy) M(g) / (F0 Teff) avec F0 =0,20 et Teff = 7,6 jours.
Calculer l'activité initiale reçue.
A = 23,4*1,4*20 / (0,2*7,6) =4,3 102 MBq.
C'est à dire environ 300 fois plus que lors d'une scintigraphie de la thyroïde.
|
|
