|
|
Un
générateur médical d'ultrasons utilisé en échographie émet des
ultrasons de fréquence f = 10,0 MHz. Cette onde est générée par trains
d'ondes d'une durée t = 2,00 µs émis à intervalle de temps T0 = 0,500 ms.
La même sonde assure l'émission d'ultrasons pendant l'excitation
électrique de l'émetteur et la réception des échos provenant de la
région anatomique explorée entre deux excitations.
Etude de la sonde.
Calculer la période Tus des ultrasons et en déduire le nombre de périodes constituant un train d'ondes.
Tus = 1/f = 1/ 107 = 1,00 10-7 s.
t / Tus = 2,00 10-6 / (1,00 10-7) =20.
Quel
nom porte le phénomène physique permettant à la sonde d'être à la fois
émettrice et réceptrice ? Expliquer succinctement cette double
propriété physique.
La piézoélectricité
découverte par Pierre et Jacques Curie, peut
être mise en évidence avec certains cristaux
anisotropes, comme le quartz.
Pour une échotomographie abdominale, on utilise un
émetteur à ultrasons, constitué d'une
lame de quartz (L) dont les faces parallèles ont
été métalisées.
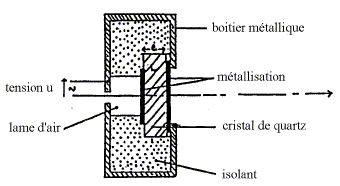
Elle vibre sous l'action d'un champ électrique
alternatif obtenu en appliquant entre les deux faces
parallèles de la lame une tension sinusoïdale u,
de fréquence de quelques mégahertz.
Inversement, une déformation du cristal provoquée par une onde
ultrasonore, induit une tension à ses bornes. L'émetteur
piezo-électrique est alors utilisé en récepteur.
Expliquer par un calcul, pourquoi on peut dire que la sonde passe donc 99,6 % de son temps de travail en réception.
(0,5 10-3 - 2,0 10-6) / (0,5 10-3) =0,996 ou 99,6 %.
|
| .
. |
.
|
Principe de la mesure de l'épaisseur d'un tissu adipeux.
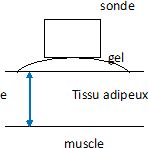
Expliquer pourquoi on doit appliquer un gel sur la peau du patient.
Un gel permet de remplacer
l'interface air-peau (eau) par les deux interfaces air-gel
et gel-tissus (eau) : les ondes sont ainsi mieux transmises.
L'épaisseur du tissu adipeux est e = 32 mm. La puissance surfacique (
ou intensité ) du faisceau d'ultrasons vaut à l'entrée de l'épiderme I0 = 94 mW cm-2.
Le coefficient d'absorption du tissu adipeux vaut a = 1,15 cm-1.
La célérité des ultrasons dans le tissu adipeux vaut c1 = 1450 m s-1.
On admet que les dimensions des détarvés sur une échographie sont de
l'ordre de grandeur de la longueur d'onde ultrasonore employée.
Quelles sont les dimensions ( en m ) des détails que l'on peut observer dans le tissus adipeux pour la fréquence utilisée ?
l = c1 / f =1450 / 107 = 1,45 10-4 m.
Calculer la durée t mise par les ultrasons pour parcourir la distance entre l'épiderme et le muscle.
t = e / c1 = 32 10-3 / 1450 = 2,2 10-5 s = 22 µs.
Montrer que l'intensité du faisceau arrivant sur l'interface tissu adipeux / muscle vaut 2,4 mW cm-2.
I = I0 exp(-a e) =94 exp(-1,15*3,2) =2,4 mW cm-2.
Calculer l'atténuation A en dB du faisceau d'ultrasons.
A = 10 log ( I0/I) = 10 log(94/2,4) ~16 dB.
|
L'impédance acoustique du muscle est Z2 =1,60 106 SI. La masse volumique du tissu adipeux est r = 952 kg m-3. Le coefficient de reflexion de l'interface tissu adipeux / mucscle se calcule par :
R = (Z1-Z2)2 / (Z1+Z2)2.
Il donne aussi le rapport entre l'intenité du faisceau réfléchi et l'intensité du faisceau incident.
Exprimer l'impédance acoustique Z1 du tissu adipeux puis le calculer en précisant sont unité.
Z1 = r
c1 avec r
en kg m-3 ; c1 en
m/s et Z en kg m-2
s-1 ou Rayl.
Z1 =952 *1450 =1,38 106 kg m-2
s-1.
Calculer
le coefficient de réflexion R. Montrer que le coefficient de
transmission est T = 99,5 %. Ces coefficients dépendent-ils du sens de
la traversée par les ultrasons de l'interface ?
R = (1,38-1,60)2 / (1,38+1,60)2 =5,45 10-3 ou 0,585 %.
R + T = 1 ; T = 1-5,45 10-3 ~0,995 ou 99,5 %.
Ces coefficients sont indépendants du sens de traversée de l'interface par les ultrasons.
Calculer l'intensité I' du faisceau revenant sur l'interface tissu adipeux / épiderme.
I' / I = R ; I' = R I = 5,45 10-3 *2,4 =1,3 10-2 mW cm-2.
|
|

