|
|
Etude du mouvement de la station.
La
station est notée S, supposée ponctuelle, évolue sur une orbite qu'on
admettra circulaire, dont le plan est incliné de 51,6° par rapport au
plan de l'équateur. Son altitude est d'environ h ~400 km.
Rayon de la terre R = 6380 km ; masse de la sation m = 435 tonnes ; masse de la terre M = 5,98 1024 kg ; G =6,67 10-11 SI.
Représenter sur un schéma : la terre et la station S, un
vecteur unitaire u orienté de la station vers la terre, la force
d'interaction gravitationnelle exercée par la terre sur S. Donner
l'expression vectorielle de cette force.
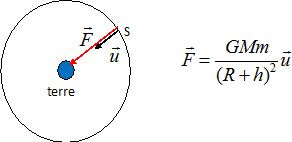
En considérant la seule action de la terre, dans le référentiel géocentrique supposé galiléen,
établir l'expression vectorielle de l'accélération as de la station.
La seconde loi de Newton conduit à :
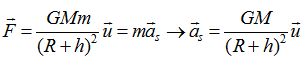
Montrer que dans le cas d'un mouvement circulaire, la valeur de la vitesse du satellite a pour expression v = (GM/(R+h))½. Calculer sa valeur.
La force de gravitation, perpendiculaire à la vitesse, ne travaille
pas. En conséquence l'énergie cinétique et la valeur de la vitesse du
satellite ne sont pas modifiées. La valeur de la vitesse étant
constante, le mouvement est uniforme.
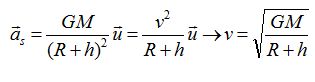
v = [6,67 10-11 *5,98 1024 / (6,38 106 + 4,00 105)]½=7,67 103 m/s.
Combien de révolutions autour de la terre un astronaute présent à bord de la station fait-il en 24 heures ?
La station décrit la circonférence 2p(R+h) à la vitesse v en T seconde.
T = 2p(R+h) / v =6,28(6,38 106 + 4,00 105) / (7,67 103) =5554 s.
Nombre de révolutions : 24*3600 / 5554 =15,55 ~15,6.
|
| .
. |
.
|
Ravitaillement de la station.
On se propose dans cette partie d'étudier le décollage de la fusée.
Dans le référentiel terrestre supposé galiléen, à l'instant t=0, la
fusée est immobile. A la ate t= 1 s, la fusée a éjecté une masse de gaz
mg à la vitesse vg. Sa masse est alors notée mf et sa vitesse vf.
On donne g = 9,78 m s-2 ; débit d'élection des gaz au décollage D = 2,9 103 kg s-1; vg = 4,0 km/s. Masse de la fusée au décollage : 7,8 102 tonnes.
Dans un modèle simplifié, on suppose que le système {fusée + gaz} est isolé.
Donner l'expression vectorielle de la vitesse de la fusée.
A
t=0, le système étant immobile, sa quantité de mouvement est nulle. Le
système étant isolé, le vecteur quantité de mouvement du système se
conserve.
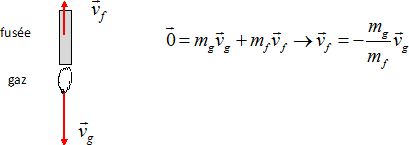
La fusée est propulsée par réaction.
Après avoir montrer numériquement que la variation de la masse de la fusée est négligeable à t = 1 s, calculer vf.
2,9
tonnes de gaz ( donc de combustible et comburant ) sont éjectés en une
seconde, valeur négligeable devant la masse de la fusée 780 tonnes.
7,8 102 -2,9 =777,1 ~ 7,8 102 tonnes.
Ecart relatif : 2,9 / 780 *100 ~0,4 %.
vf = 2,9 /(7,8 102) *4,0 103= 14,87 ~15 m/s.
|
|
Etude plus réaliste du décollage.
En réalité la vitesse vf est très inférieure à celle calculée ci-dessus.
Quelle force n'aurait-on pas dû négliger ?
En réalité, le système n'est pas isolé :
On aurait dû tenir compte du poids du système et des forces de frottement dûes à l'air.
On considère désormais le système {fusée }. Il est soumis à son poids P et à la poussée des moteurs F = Dvg.
Montrer que le produit Dvg est homogène à une force.
D s'exprime en kg s-1 et vg en m s-1 ; Dvg s'exprime donc en kg m s-2, c'est à dire une masse fois une accélération, donc à une force.
A l'équivalence la quantité de matière d'aspirine est égale à la
quantité de matière de soude :
Vérifier par une application numérique que la fusée peut décoller.
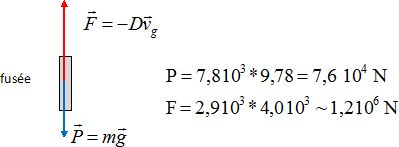
La poussée des moteur étant supérieure au poids de la fusée, celle-ci peut décoller.
|
|