|
|
Partie A.
Maurice s'interroge sur les notions de braquet, de développement, de «
fréquence de pédalage » et de « force motrice » de sa bicyclette (sa «
randonneuse »).Aidez-le à comprendre.
Expliquer la signification d'un braquet 30/15.
Le braquet, noté Br, est le rapport entre le nombre de dents de la couronne du pédalier ou
plateau et le nombre de dents de la couronne de la roue libre ou pignon fixé sur la roue arrière.
Un braquet 30/15 : le plateau compte 30 dents et le pignon 15 dents.
Pourquoi le braquet est-il exprimé sans unité ?
Le braquet étant le rapport de deux grandeurs ayant la même unité, Br est sans unité.
Avec un plateau de 43 dents, le braquet idéal d’un cyclotouriste que l’on notera Br2 doit être le plus proche possible de 2,5.
Calculer le développement D (en m) de la bicyclette lorsque le braquet est Br =43 / 17 = 2,53.
Le développement est D = Br 2π r avec r rayon de la roue du vélo, r = 0,315 m.
D =2,53 *2*3,14 *0,315 =5,01 m.
En déduire la fréquence de pédalage fp de Maurice, exprimée en tour.min–1, lorsqu’il roule à une vitesse v = 22,5 km.h–1 ( la fréquence de pédalage correspond aux nombres de tours de pédalier effectués en une minute ).
v = 22,5 *1000 / 60 = 375 m / min.
A chaque tour tour de pédalier, le cycliste avance de 5,01 m ;
par suite la fréquence de pédalage est : fp = 375 / 5,01 ~75 tr / min.
Cette valeur est en accord avec la fréquence de pédalage des cyclotouristes ( 70 à 80 tours de pédalier par minute ).
La force motrice
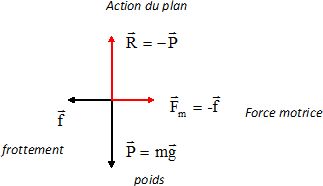
Représenter à l'échelle le vecteur force motrice Fm qui permet à Maurice de rouler à vitesse constante sur une route rectiligne et horizontale. Justifier la réponse.
Dans un mouvement
rectiligne uniforme, la somme vectorielle des force appliquées au
système { vélo + cycliste } doit donc être nulle.
|
.
|
Partie B. L’accumulateur Li-Mn.
Vérifier
si le choix du type d'accumulateur (batterie) est judicieux pour
réaliser un trajet journalier moyen et pour recharger l’accumulateur.
Maurice veut faire 2400 km en 30 jours, c'est à dire, en moyenne, 80 km/jour.
D’après l’annexe B1, cette distance journalière correspond à l’autonomie minimale du dispositif retenu.
De plus, 7 heures ( durant la nuit ) sont nécessaires pour la recharge complète.
Préciser à quelles grandeurs physiques correspondent les indications 8,8 Ah et 422 Wh qui figurent sur le descriptif technique.
La capacité de la batterie est égale à Q = 8,8 ampère heure.
L’énergie stockée dans la batterie est égale à 422 Wh..
Calculer
l’intensité I du courant constant pouvant être débité pendant un durée
de 6 h jusqu’à la décharge complète de l’accumulateur.
I = Q / t = 8,8 / 6 ~1,5 A.
Calculer
la durée Δt d’utilisation de l’accumulateur (jusqu’à sa décharge
complète) si la puissance consommée par le moteur et les équipements
vaut P = 140 W.
Dt = énergie stockée ( Wh) / puissance (W) = 422 / 140 =3,0 heures.
Compléter le document en indiquant :
les sens de déplacement des porteurs de charges (électron et ion
lithium) et le sens du courant I lorsque la batterie se décharge ;
les polarités de l'accumulateur ; les noms des électrodes et des réactions qui s'y produisent.
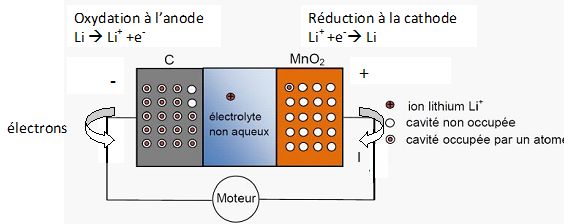
Lors de la charge de l’accumulateur, les ions lithium Li+ migrent à travers l'électrolyte, pour atteindre l'électrode en carbone, où ils
se réduisent en atome de lithium.
La réaction inverse se produit lors de la décharge : oxydation du lithium sur l'électrode de carbone selon Li = Li+ + e -.
L'électrode de carbone est donc négative. Le courant circule dans le sens contraire de celui des électrons.
A la cathode positive, on observe une réduction des ion Li+ lors de la décharge.
Lors de la recharge de l'accumulateur, donner la nature (continue ou alternative) et la valeur de la tension U.
La tension U est continue et vaut 48 V.
Définir le moment de la force F en donnant son expression et en complétant le document.
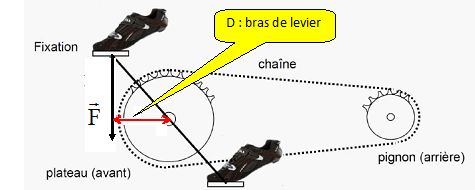
Le moment, noté M, de la force F est égal à M = F D ( force en newton et D en mètre ).
Donner
la relation du moment C du couple moteur en fonction de la puissance
mécanique P du moteur et de la vitesse de rotation ω (rad.s-1). Calculer la vitesse de rotation ω (en rad.s-1) puis en tr.min -1) si le moment du couple moteur vaut 40 N.m pour une puissance mécanique de 100 W.
P = C w ; w = P/C = 100 / 40 = 2,5 rad s-1.
soit 2,5 *60 / (2*3,14) ~ 24 tr min-1.
|
La
route est rectiligne et horizontale, Maurice circule à vitesse
constante, il n'y a pas de vent, le moteur développe une puissance de
100 W, le moment moyen du couple (supposé constant) exercé par le
cycliste vaut 30 N.m, la vitesse angulaire du pédalier est 3,5 rad.s-1.
Calculer pour une durée de 15 min :
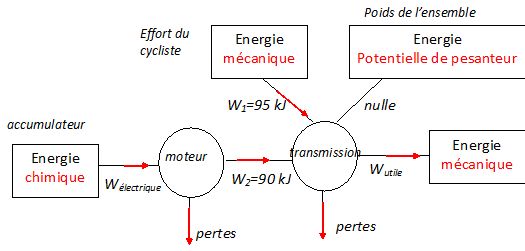
W1 : travail fourni par Maurice : W1 = P Δt = C w Dt = 30 * 3,5 * 15 x 60 ~ 95 kJ
W2 : travail fourni par le moteur électrique : W2 = P Δt = 100 *15 * 60 = 90 kJ.
W3 : travail du poids : W3 = 0 J. ( une force perpendiculaire à la vitesse ne travaille pas ).
Compléter la chaîne énergétique suivante.
La route est en descente. Maurice ne pédale pas et ajuste son freinage pour maintenir sa vitesse constante à 35 km.h–1.
La législation impose que l’assistance électrique cesse à partir d’une vitesse de 25 km/h.
Pour des raisons de sécurité, le moteur passe mode débrayé (il se
coupe) lorsque l'on actionne les freins et bascule en mode récupération
d'énergie (il fonctionne en alternateur).
Indiquer uniquement les sens des transferts.
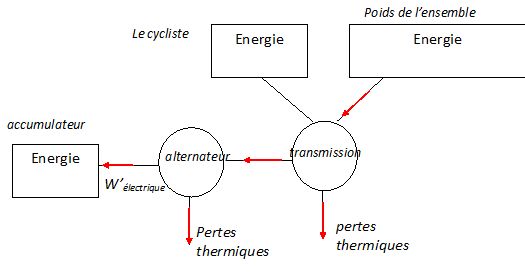
|
|
Sachant que la puissance maximale utile du V.A.E. de Maurice est de 250 W, déterminer le pourcentage maximal de la pente sur laquelle Maurice peut rouler à 15 km.h-1 en maintenant sa puissance musculaire égale à 60 W.
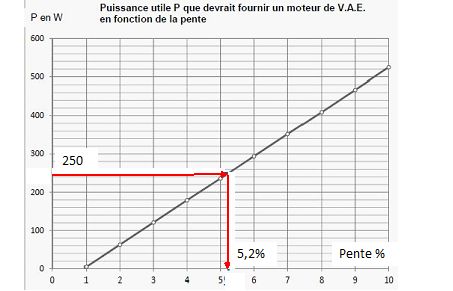
Déterminer la puissance musculaire que devrait avoir Maurice pour maintenir sa vitesse constante à 15 km/h sur une montée à 6 % ?
L'assistance électrique ne peut fournir que 250 W, alors qu'il en faudfrait 300 d'après le graphe.
Le cycliste doit donc fournir : 50 + 60 = 110 W.
L’ascension de l’Alpe d’Huez (14,4 km ; 1120 m de dénivelé ; 21 virages
et une pente moyenne de 8 %) avec le V.A.E. à une vitesse de 10 km/h,
nécessite une puissance de 308 W (puissance du
moteur 248 W, puissance musculaire 60 W). Maurice souhaite déterminer
la puissance musculaire qu'il aurait dû développer sans assistance
électrique pour effectuer ce trajet avec sa randonneuse et ses
bagages dans les mêmes conditions. Pour cela vous devez :
Déterminer le travail du poids P du système {Maurice, vélo, bagages} lors de cette ascension. Msystème = 97,5 kg ; g = 9,81 SI.
Le travail du poids est résistant en montée : Wpoids = -Msystème g H = -97,5*9,8*1120 = -1,07 106 J.
Sachant que l'énergie perdue lors de cette ascension, en raison de l'ensemble des frottements, est de 130 kJ, calculer l'énergie musculaire E qu'aurait dû développer Maurice.
L’énergie mise en jeu par le cycliste sert à compenser le travail du poids et l’énergie perdue par les frottements :
E = 1,07 106 + 1,30 105 = 1,20 106 J.
Calculer
la durée du trajet et en déduire la puissance musculaire qu'aurait dû
développer le cycliste pour faire l’ascension avec une vitesse
constante de 10 km/h.
Le cycliste a parcouru 14,4 km à la vitesse de 10 km/h, la durée de la montée est 14,4 / 10 = 1,44 heure ou 1 h 26 min.
Puissance musculaire = 1,2 106 / (1,44*3600) =231 W.
|





