|
|
La
bouteille de Leyde est considérée comme l'ancêtre du condensateur. Elle
est formée d'une électrode supérieure constituée de feuilles d'or
suspendues à l'aide d'une chaîne à l'intérieur d'une bouteille en
verre. Une deuxième électrode est une feuille métallique d'étain
enveloppant l'extérieur de la bouteille.
Reliée à un générateur ( à
friction ), la bouteille de Leyde peut accumuler des charges
électriques. En, 1853, Sir William Thomson étudie un circuit comprenant
une bouteille de Leyde et une bobine. Il s'aperçoit qu'avec des bobines
de résistance interne suffisamment faible, il apparaît des oscillations
électriques peu amorties dans le circuit.
A propos de la bouteille de Leyde.
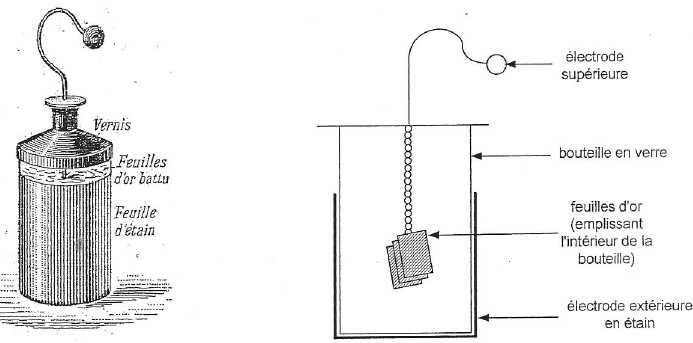
Indiquer le(s) constituant(s) de la bouteille jouant le rôle des armatures.
Les feuilles d'or et l'enveloppe extérieure d'étain jouent le rôle des armatures.
Le tableau ci-dessous regroupe les mesures de la tensio électrique uc aux bornes d'une bouteille de Leyde en fonction de la charge q portée par son armature positive.
| uc (V) | 0 | 2,0 | 4,0 | 6,0 | 8,0 | 10 | | q(C) | 0 | 1,9 10-9 | 4,2 10-9 | 6,1 10-9 | 7,9 10-9 | 10,1 10-9 | | C = q/uc ( F) | xxx | 9,5 10-10 | 1,05 10-9 | 1,0 10-9 | 9,9 10-10 | 1,0 10-9 |
Tracer la courbe q = f(uc) ; déduire de la courbe la relation existant entre q et uc et déterminer la capacité du condensateur équivalent à cette bouteille.
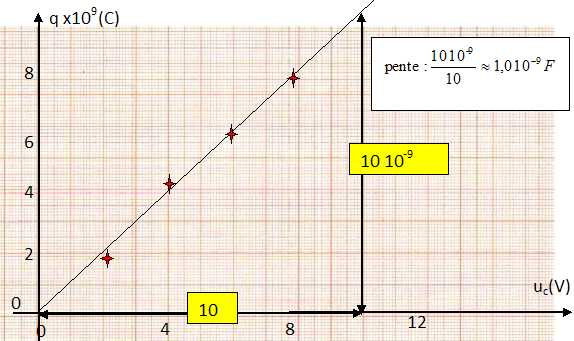
La charge q et la tension uc sont proportionnelles. La constante de proportionnalité est la capacité du condensateur proche de 1,0 nanofarad.
Reproduction de l'expérience de Thomson au laboratoire.
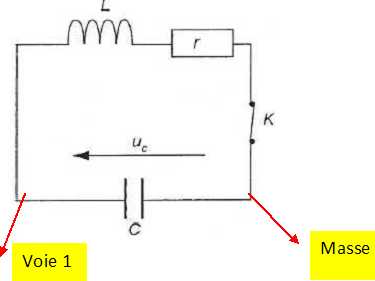
On
réalise le circuit suivant comprenant une bouteille de Leyde assimilée
à un condensateur de capacité C inconnue, une bobine d'inductance L =
0,1 H et de résistance interne r ainsi qu'un interrupteur K. On note uc la tension aux bornes du condensateur. Le condensateur est initialement chargé. A l'instant initial t0=0, l'interrupteur est fermé.
Pour visualiser la tension uc au cours du temps, on utilise un système automatique d'acquisition de données.
Représenter les branchements à réaliser pour visualiser uc.
|
| .
. |
.
La courbe ci-dessous représente l'évolution temporelle de la tension uc lorsque la valeur de la résistance interne de la bobine est faible.
Quel est le nom du régime observé ? Donner la cause de la diminution de l'amplitude des oscillations.
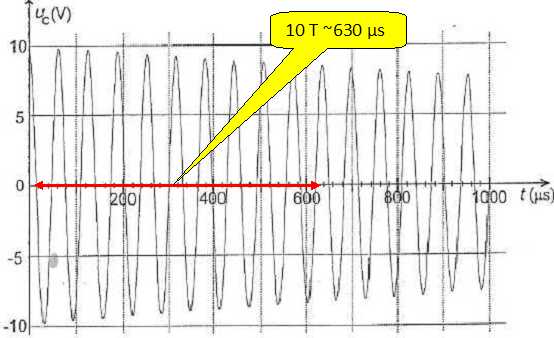
Le régime est pseudo-périodique.
Au cours des échanges d'énergie entre bobine et condensateur, une
partie de celle-ci est perdue par d'effet Joule dans le circuit.
On mesure une pseudo-période T = 63 µs.
Expliquer comment il faut opérer pour déterminer précisément cette valeur.
On mesure une dizaine de pseudo-périodes, voir schéma ci-dessus.
Modélisation du circuit réalisé par Thomson.
On
considère dans cette partie que la bobine est idéale, c'est à dire que
sa résistance interne est nulle. L'objectif de cette question est de
déterminer la capacité de la bouteille de Leyde.
Représenter en convention récepteur la tension uc aux bornes du condensateur et uL aux bornes de la bobine.
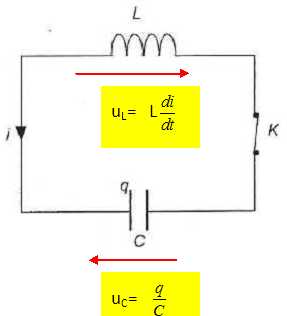
Etablir la relation entre l'intensité i et la tension uc.
i = dq/dt et uc = q/C ; duc/dt = 1/C dq/dt = i / C ou i = Cduc/dt
En déduire l'expression de la tension uL en fonction de la tension uc.
uL = Ldi/dt avec di/dt = Cd2uc/dt2 d'où : uL = LCd2uc/dt2.
Montrer que l'équation différentielle vérifiée par la tension uc peut s'écrire : 1/(LC) uc +d2uc/dt2=0.
Additivité des tensions : uc+uL=0.
uc + LCd2uc/dt2 =0 ; 1/(LC) uc +d2uc/dt2=0. (1).
Une solution de cette équation différentielle s'écrit : uc(t) = Um cos(2pt/T0).
Que représentent les grandeurs Um et T0 ?
Um : amplitude en volt ; T0 : période propre de l'oscillateur.
Montrer que T0 = 2 p(LC)½.
duc(t) /dt = -Um 2p/T0 sin(2pt/T0) ; d2uc/dt2= -Um (2p/T0 )2cos(2pt/T0) = -(2p/T0 )2uc.
Repport dans (1) : 1/(LC) uc-(2p/T0 )2uc = 0 ; 1/(LC)-(2p/T0 )2 = 0 ; T0 = 2 p(LC)½.
Vérifier par analyse dimensionnelle la cohérence de l'expression de T0.
2 p est sans dimension ; L est une énergie divisée par le carré d'une intensité ; L 'exprime en J A-2.
C
est le carré d'une charge divisée par une énergie soit le carré d'une
intensité fois le carré d'un temps divisé par une énergie ; C
s'exprime en A2s2 J-1.
LC s'exprime donc en s2 et (LC)½ s'exprime en seconde.
Trouver l'expression littérale donnant C en fonction de T0 et L ; calculer C.
T02 = 4 p2 LC ; C = T02 /(4 p2 L) = (63 10-6)2 / (4*3,142 *0,10) =1,0 10-9 F, en accord avec la valeur trouvée précédemment.
Aspect énergétique de l'expérience de Thomson.
Donner les expressions de l'énergie Ec emmagasinnée dans un condensateur et EL emmagasinnée dans une bobine.
Ec =½Cuc2 ; EL = ½Li2.
La
figure ci-dessous représente l'évolution au cours du temps de l'énergie
emmagasinnée par un des dipôles ( bouteille de Leyde ou bobine ).
Préciser quel dipôle en justifiant.
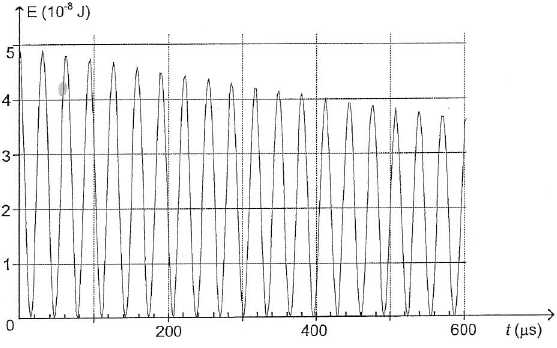
Initialement le condensateur est chargé et l'intensité du courant est nulle. Le condensateur stocke à t0 toute l'énergie du dipôle LC. D'après le graphe ci-dessus, l'énergie initiale n'est pas nulle.
Le graphe représente donc l'énergie stockée par la bouteille de Leyde.
|
.





