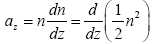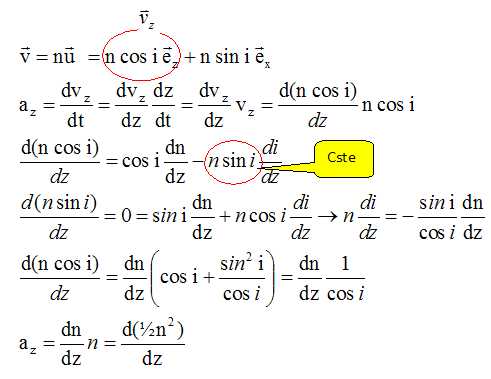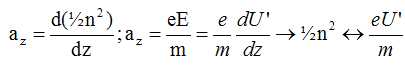Réfraction, mirage, réfraction électronique : Concours général  1993. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. ..

. .

Réfraction. Un milieu transparent homogène et isotrope est caractérisé par son indice de réfaction n. Rappeler la relation entre l'indice, la vitesse de la lumière dans le milieu et la vitesse de la lumière dans le vide. n = cvide / vmilieu. Rappeler en quelques mots en quoi consiste le phénomène de réfraction. Lorsque la lumière rencontre la surface séparant deux milieux transparents d'indice de réfraction diférents, la lumière passe dans le second milieu en changeant de direction à l'exception de l' incidence normale. Rappeler les lois de Descartes pour la réfraction. Rayons incident, réfléchi et réfracté sont coplanaires. nair sin i = N sin r ; N sin r' = nair sin i'. Soit un empilement de lames à faces parallèles de faible épaisseur avec n1 < n2 < n3. Dessiner la marche d'un rayon lumineux à travers l'empilement. Soit maintenant un milieu transparent dont l'indice n(z) est une fonction continue de la seule coordonnée z.  En vous fondant sur la question précédente, donnez l'allure de la marche d'un rayon lumineux traversant le milieu si dn/dz >0. Que peut-on dire de la quantité n sin i ? Connaissez-vous des exemples illustrant cette situation ? L'indice de réfraction varie de manière continue, c'est à dire que les plans précédents se rapprochent les uns des autres. La ligne brisée tend vers une courbe continue. n sin i =constante. Cette situation se rencontre dans les mirages. Réfraction électronique. 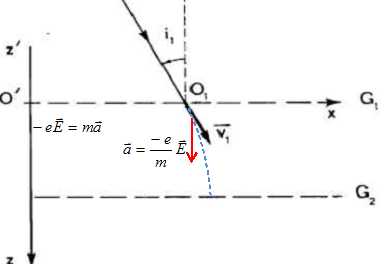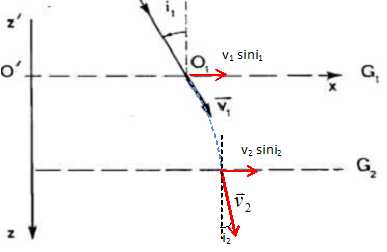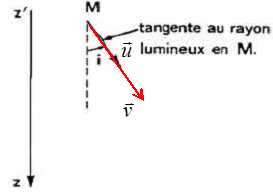Un filament de tungstène chauffé émet, par effet thermoélectronique, des électrons ayant une vitesse pratiquement négligeable. Le filament ou cathode est porté à un potentiel VC < 0. Une anode, percée d'une petite ouverture O est portée au potentiel VA = 0. Calculer la vitesse des électrons en O en fonction de la charge élémentaire e, de la masse m d'un électron et de la tension U = VA – VC. Application numérique : U = 1,0 kV. Le poids des électrons est négligeable devant la force électrique F = eE. Le travail moteur de cette force vaut W = eU. Appliquer le théorème de l'énergie cinétique : ½mv2-0 = eU ; v = (2eU/m)½. v = (2*1,6 10-19 * 1000 / (9,1 10-31))½ =1,875 107 ~1,9 107 m/s. Deux grilles métalliques G1 et G2 planes et parallèles sont soumises à la tension U' = VG2 − VG1 > 0. Un faisceau homocinétique d'électrons, de vitesse v1 arrive sur G1 en O1 avec l'incidence d'angle i1. Donner les caractéristiques du champ électrostatique entre les grilles, le représenter sur une figure. Donner, sans démonstration, la nature de la trajectoire d'un électron M entre les grilles. Représenter l'allure de cette trajectoire. L'électron étant soumis à la force électrique constante, la vitesse initiale n'étant pas colinéaire à la force, sa trajectoire entre les deux grilles est parabolique. 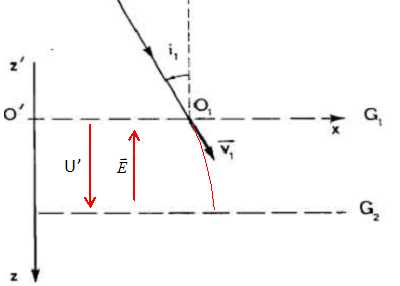Quelle est la nature du mouvement de la projection de M sur l'axe O'x parallèle aux grilles ? En déduire la relation entre la vitesse v de l'électron et l’angle i que fait le vecteur vitesse avec O'z.  Quelle est la relation entre i1, i2, v1 et v2 où i2 est l'angle de sortie en G2 et v2 la vitesse en G2 ? La composante de l'accélération étant nulle suivant O'x, le mouvement  de la projection de M sur l'axe O'x est rectiligne uniforme. vx = v sin i = v1 sin i1 = v2 sin i2 = constante. Quelle analogie avec l'optique ces résultats vous suggèrent-ils ? La relation v1 sin i1 = v2 sin i2 est analogue avec la loi de Descartes. On se propose de développer l'analogie précédente dans le cas d'un milieu transparent et isotrope dont l'indice est fonction de la seule coordonnée z.  On introduit à cet effet une particule fictive dont la trajectoire devra se confondre avec le rayon lumineux. On attribue à cette particule fictive une masse unité et une vitesse v= n où n est l'indice du milieu au point M considéré et u le vecteur unitaire tangent en M au rayon lumineux considéré et dirigé dans le sens de propagation. Justifier brièvement ces choix. En considérant le mouvement de la particule fictive projeté sur Oz, montrer que l'accélération de ce mouvement est : Quelle est la correspondance entre l'indice n et le potentiel U’M en M dans le problème d'électrostatique ? Quel est l'intérêt d'une telle correspondance ? On choisit n en fixant la valeur de U'.

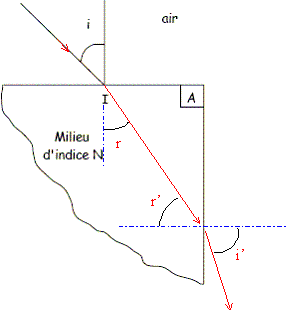
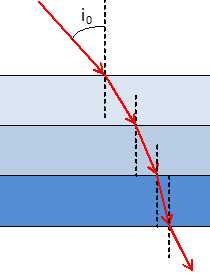
Au voisinage d'un sol chauffé, la température de l'air varie avec la distance z au sol . Dans quel sens s'effectue cette variation lorsqu'on s'éloigne du sol ? Justifier. La température est plus élevée au niveau du sol chauffé par le soleil et décroît avec l'altitude. Prévoir qualitativement le sens de variation de l'indice de réfraction de l'air au voisinage du sol. Justifier. La densité de l'air chaud est plus faible que celle de l'air froid. L'indice de réfraction de l'air chaud est plus proche de l'indice du vide. L'indice de réfraction augmente avec l'altitude.  On admet que cette variation est approximativement de la forme n(z) = n0 + az, |az|<<n0 et où α est une constante.  Quelle est, dans cette approximation, la forme des rayons lumineux ? Faire un dessin représentant un rayon lumineux émis parallèlement au sol. Quel type de phénomène peut-on expliquer de la sorte ? az = n dn/dz = ( n0 + az ) a ; z" -a2z - an0 = 0 (1). Equation caractéristique associée : r2 -a2r - an0 = 0 ; discriminant : D = a4+4 an0. Solutions : ß1 = (a2+D½) / 2 ; ß2 = (a2-D½) / 2 ; Solution générale de (1) : z(t) = A exp (ß1t) + B exp(ß2t) où A et B sont des constantes. Au sol : z(0)= A + B = 0 ; B = -A soit z(t) = A( exp (ß1t) -exp (ß2t) ). Un rayon lumineux émis parallèlement au sol ( altitude z constante ), reste parallèle au sol. Un rayon non parallèle au sol est dévié, d'où l'explication des mirages. I.6. Soit un dioptre plan séparant deux milieux transparents. homogènes et isotropes d'indices respectifs n1 et n2. Montrer que le parcours de la lumière est parmi ceux reliant deux points donnés A et B, celui qui rend le temps de parcours minimal. On pourra prendre comme variable l'angle d'incidence i1 et noter que HH' a une valeur donnée. 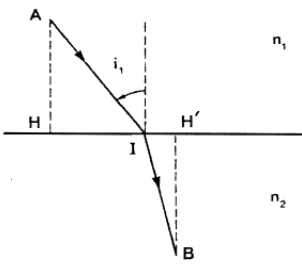Temps de parcours : t = AI /v1 + IB / v2 =  n1 AI / c + n2 IB / c. AI = AH / cos i1 ; IB = H'B / cos i2 ;  t =1/c ( n1 AH / cos i1 + n2 H'B / cos i2 ). dt/di1 = 1/c(n1sin i1AH / cos2 i1 + n2 sin i2 H'B / cos2 i2 di2 / di1). (1). HH' = HI + IH' = AH tan i1 + H'B tan i2=constante. dHH'/dt = 0 =  AH / cos2 i1 + H'B / cos2 i2 di2 / di1=0 ;  (1) s'écrit alors : dt/di1 =1/c (n1sin i1AH / cos2 i1 -n2 sin i2AH / cos2 i1)= 1/c AH / cos2 i1(n1sin i1-n2 sin i2). Le temps de parcours est minimal si : dt/di1 =0 si (n1sin i1-n2 sin i2) =0 soit n1sin i1=n2 sin i2.

menu