|
|
A propos du laser.
Montrer en utilisant la relation c = l × n que doubler la fréquence permet de diviser par deux la longueur d’onde émise initialement par le laser.
c est une constante la célérité de la lumière dans le vide.
La longueur d'onde et la fréquence sont deux grandeurs inversement
proportionnelles : doubler la fréquence, c'est diviser par deux la
longueur d'onde.
Indiquer une propriété particulière du laser pulsé.
Le laser pulsé émet des impulsions lumineuses très brèves (20
picosecondes), d’une puissance instantanée fantastique, l'énergie étant
concentrée sur un temps très court.
Justifier l’affirmation d’Étienne SAMAIN : "le laser émet des impulsions de puissance instantanée fantastique".
Données : chaque impulsion émet une énergie E = 200 mJ.
La puissance p d’une impulsion est reliée à l’énergie E émise pendant la durée Dt d’une impulsion :
p = E / Dt = 200 10-3 / (20 10-12) =1,0 1010 W émis en une durée très courte.
Cette valeur est très supérieure à la puissance des appareils électriques de la vie courante.
Estimer le nombre de photons émis à chaque impulsion en direction de la Lune.
On donne l = 532 nm dans le vide.
Energie d'un photon émis par le laser : E = h c / l = 6,63 10-34 *3,00 108 / (532 10-9) =3,74 10-19 J.
Nombre de photons émis par impulsion : 0,200 / (3,74 10-19) =5,34 1017.
L’utilisation des valeurs numériques des grandeurs mises en jeu
pour ce calcul n’est pas nécessaire ; une estimation à l’aide des
ordres de grandeur de celles-ci sera privilégiée.
Autre méthode : l'ordre de grandeur de l'énergie d'un photon est de quelques électrons volts, ou encore de l'ordre de 10-19 J. Le nombre de photons émis par une impulsion est de l'ordre de 0,2 / 10-19 ~1018.
Calculer le rayon de la tache lumineuse obtenue sur la Lune.
Tout faisceau lumineux diverge. À son départ, le faisceau laser a un
diamètre D de deux mètres (…). La diffraction provoque donc une faible
divergence, de un millionième de radian, soit un élargissement du
faisceau de l’ordre du micromètre par mètre parcouru. Mais comme la
distance Terre-Lune mesure la bagatelle d’environ 400 000 kilomètres,
l’effet à l’arrivée est important.
La diffraction se produisant de la même façon pour le faisceau retour, on ne détecte
qu’une infime partie de cette lumière réfléchie : environ 2 x 10-18 millijoule par impulsion envoyée.
D’après Pour la Science, dossier n°53, octobre-décembre 2006, La lumière, c’est combien de photons ?
Jean-Michel COURTY et Nicolas TREPS, Université Pierre et Marie Curie, Paris.
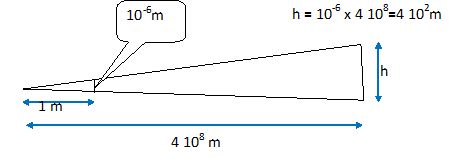
Le rayon de la tache lumineuse obtenue sur la lune est d'environ 400 m, c'est à dire 400 fois plus que le diamètre
initial du faisceau. Même pour pour une divergence très faible, au bout
d'une distance très grande, la tache observée est énorme.
|
| .
. |
.
|
À propos de la mesure de la distance Terre-Lune.
Date
heure min ns
Durée aller retour en 10-13 s Distance terre - lune(km)

Par
quel calcul sont obtenues les distances Terre-Lune de la dernière
colonne du tableau ? Expliciter celui manquant dans le tableau de
mesures, puis calculer sa valeur, en se contentant de la précision de la calculatrice.
Multiplier la célérité de la lumière dans le vide par la durée d'un aller ( ou d'un retour ) :
299 792 458 *24164440511979 10-13 / 2 =3,622158508 108 m = 362215,8508 km.
D’après le nombre de chiffres significatifs fournis par l’OCA dans ses fichiers de données,
avec quelle précision la distance Terre-Lune est-elle mesurée actuellement ?
10 chiffres significatifs sont donnés, soit une précision sur la distance terre-lune de quelques centimètres.
A votre avis, quel type d’horloge peut permettre d’atteindre une telle précision sur les durées de parcours des impulsions ?
Seule une horloge atomique permet d'atteindre une telle précision.( ±5 picosecondes).
Proposer deux hypothèses à considérer pour tenter d’expliquer les écarts observés sur la mesure de la distance Terre-Lune.
L'orbite de la lune autour de la terre n'est pas parfaitement circulaire.
La vitesse de la lumière change selon
l'altitude et les diverses couches d'air traversées.
Le pointage du télescope sur le
réflecteur doit rester très précis pendant toute la durée de la mesure
malgré les mouvement de la Terre et de la lune.
|
|