|
|
Le laser, faisceau de lumière cohérente.
La
lumière émise par une source laser provient de l'émission stimulée
d'atomes excités par pompage optique. On a représenté sur le schéma
ci-dessous deux niveaux d'énergie d'un atome présent dans la cavité de
la source laser.
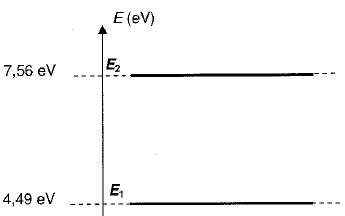
Dans quel niveau d'énergie l'atome est-il le plus excité ?
L'énergie E2 est supérieure à l'énergie E1. L'atome au niveau E2 est donc dans l'état le plus excité.
Quelle
est la valeur de la longueur d'onde de la radiation lumineuse qu'il
faut envoyer sur l'atome pour provoquer une émission stimulée de cet
atome ?
l = hc /(E2-E1) = 6,62 10-34*3,00 108/( (7,56-4,49) *1,6 10-19) =4,04 10-7 m = 404 nm.
Quelle est la longueur d'onde de la radiation émise par l'atome ?
On peut aussi favoriser la désexcitation d’un
électron en envoyant sur l’atome excité
une lumière dont la longueur d’onde correspondant à
l’énergie de transition entre les deux
états électroniques. On appelle ce
phénomène l’émission
stimulée (ou émission induite).
L’émission stimulée d’un atome ou
d’une molécule donne un nouveau photon qui a
exactement les mêmes fréquence, phase et
direction que le photon incident.
lphoton émis=404 nm.
Stockage des informations sur le disque laser.
Pourquoi dit-on que l'informationn est stockée sur le disque sous forme binaire ?
Le disque est composé d'une surface
réfléchissante sur laquelle sont
aménagées des cavités de
matériau transparent homogène
d'épaisseur e et d'indice de réfraction
n.
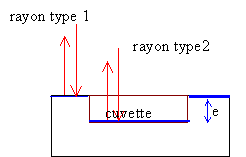
Seuls deux états sont possibles, d'où le nom binaire.
Si le faisceau est totalement réfléchi par la
surface du disque, la différene de chemin optique
est nulle : les interférences sont constructives. Même chose si le rayon est totalement
réfléchi par le fond d'une cuvette. On attribue cet état à la valeur binaire 0.
Si le faisceau passe de la surface du disque à un creux, les
interférences sont destructives. On attribue à cet état la valeur
binaire 1.
|
.
|
On a représenté la tension issue du microphone qui a permis l'enregistrement du son sur le disque.
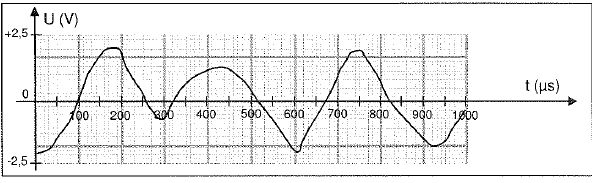
Cette tension forme-t-elle un signal numérique ou analogique ? Justifier ?
Toutes les valeurs de la tension sont possibles ; la courbe ne présente pas de discontinuité : il s'agit d'un signal analogique.
Un signal numérique varie de façon discontinue dans le temps.
Pour lire le disque et entendre de la musique qui a été enregistrée,
l'information qu'il contient doit être transformée en une tension qui
alimente les haut-parleurs.
On a représenté la tension envoyée par le lecteur CD aux bornes du
haut-parleur qui diffère sensiblement de la précédente tension
enregistrée par le microphone.
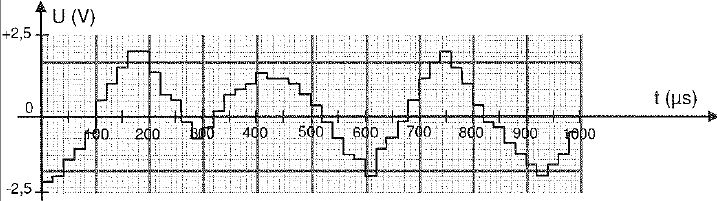
Déterminer la fréquence d'échantillonnage du convertisseur numérique-analogique.
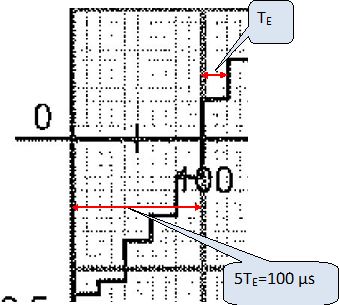
TE = 20 µs = 2,0 10-5 s ; fE = 1/TE = 1/(2,0 10-5) = 5,0 104 Hz = 50 kHz.
Comment
faudrait-il modifier cette fréquence pour que le signal envoyé au
haut-parleur se rapproche davantage de celui délivré par le microphone ?
Il faudrait augmenter la fréquence d'échantillonnage.
Lecture des informations sur un disque laser.
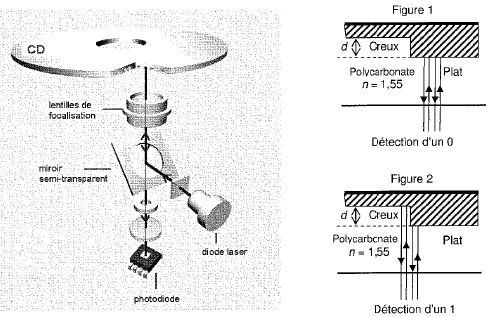
Le faisceau lumineux, constitué d'une lumière monchromatique de longueur d'onde l0
dans le vide est émis par la diode laser. Il traverse une couche
protectrice transparente en polycarbonate dont l'indice est n = 1,55,
puis il est réfléchi par le disque et détecté par la photodiode.
Lors de la détection d'un zéro, le faisceau est entièrement réfléchi
par un plat ou par un creux. Touts les rayons composant le faisceau ont
donc parcouru le même trajet. Lors de la détection d'un 1, le faisceau
laser passe d'un plat à un creux ou inversement. Une partie du faisceau
est alors réfléchie par un plat et l'autre par un creux. Tous les
rayons composant le faisceau n'ont pas parcouru le même trajet.
On note DL la différence de parcours des deux parties du faisceau qui se superposent et interfèrent lors de leur détection.
Dans le polycarbonate la longueur d'onde de la lumière est l = l0 / n.
Donner la condition que doit vérifier DL pour que les interférences soient destructives.
La différence des distances parcourues par les
rayons se réfléchissant sur un plat et ceux se réfléchissant sur un creux est égale à 2 fois l'épaisseur
de la cuvette soit 2d.
les interférences sont destructives si cette différence de marche est un multiple impair de la demi-longueur d'onde.
DL=2d =(2k+1)l/2. ( k est un entier ).
Montrer que la profondeur minimale d du creux s'exprime en fonction de l par la relation d = l/4.
Pour k=0 : 2 d = l/2 soit d = l/4.
Calculer d si l0 = 780 nm.
d =l0/(4n) =780/(4*1,55) =126 nm.
Dans quel cas le capteur reçoit-il plus de lumière. Justifier.
La détection d'un 1 correspond aux interfférences destructives, c'est à dire à un minimum de lumière.
Lors de la détection d'un zéro, le capteur reçoit donc le maximum de lumière.
|
Intérêt de la technologie Blu-ray.
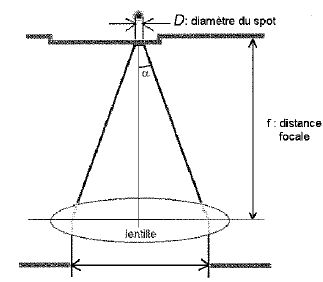
Ouverture numérique NA = sin a. Diamètre D du spot sur l'écran : D = 1,22 l0/NA.
Justifier l'appellation "Blu-ray" en faisant référence à la longueur d'onde du faisceau l0 = 405 nm.
La longueur d'onde du faisceau appartient à la teinte violette du domaine visible.
Quel est le phénomène qui empèche d'obtenir une largeur de faisceau plus faible ?
La diffraction des ondes lumineuses sur des obstacles dont les dimensions sont de l'ordre de grandeur de la longueur d'onde.
Vérifier que le diamètre D du spot est compatible avec la distance 2l qui sépare trois ligne sur le disque. l = 0,30 µm ; NA = 0,85.
D =1,22 *405 10-9 /0,85 ~5,8 10-7 m =0,58 µm.
D < 2l, le diamètre du spot est compatible.
Comment est-il possible d'améliorer la capacité de stockage du disque sans modifier sa surface ?
- Diminuer la longueur d'onde du faisceau laser, c'est augmenter la finesse de la gravure.
- Graver les informations sur plusieurs couches, la lentille permettant de focaliser la lecture sur une couche.
Un disque Blu-ray peut contenir jusqu'à 46 Gio de données, soit environ 4 heures de vidéo haute définition ( HD). 1Gio = 230 octets ; 1 octet = 8 bits ; 1 Mibit = 220 bits.
Calculer le débit binaire ( Mibit/s ) de données numériques dans le cas de la lecture d'une vidéo HD.
46 Gio =46 *230 = 4,94 1010 octets ou 8*4,94 1010 =3,95 1011 bits ou 3,76 105 Mibit.
4 h = 4*3600 s = 1,44 104 s ; débit : 3,76 105 /( 1,44 104) ~26 Mibit/s.
La HT utilise des images de résolution d'au moins 720 pixels en hauteur
et 900 pixels en largeur. Chaque pixel nécessite 24 bits de codage ( 8
par couleur primaire ).
Montrer que la taille numérique d'une image non compressée est d'environ 15 Mibit.
720*900*24 = 1,55 107 bits ou 1,55 107 /220 =14,8 ~15 Mibit.
Combien d'images par seconde peut-on obtenir sur l'écran de l'ordinateur avec le débit binaire calculé ci-dessus.
26 /15 = 1,8. ( moins de deux images ).
Pour éviter l'effet de clignotement, la projection vidéo nécessite au moins 25 images par seconde.
Pourquoi faut-il réduire la taille des images à l'aide d'un protocole de compression d'images ?
Une image non compressée est de trop grande taille ( 15 Mibit) pour
être lue rapidement, attendu qu'il faut projeter 25 images par seconde.
|
|