De la liaison covalente à la spectroscopie infrarouge, bac S Antilles 09/2013.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. ..
 


Les vibrations des liaisons de valence sont à l'origine des spectres d'absorption dans l'infrarouge proche. Une molécule absorbe de façon intense les ondes électromagnétiques dont la fréquence est proche d'une valeur appelée " fréquence propre de vibration" de la liaison covalente. Les atomes liés se mettent alors à vibrer autour de leur position d'équilibre. Un modèle simple de la liaison chimique covalente qualifié de " modèle à oscillateur harmonique" assimile la liaison entre deux atomes à une liaison solide-ressort.

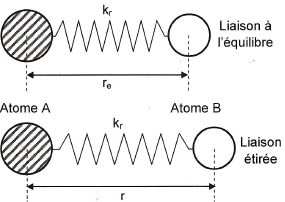
Une liaison peut être assimilée à un ressort de constante de raideur kr et de longueur à l'équilibre re.
Période propre d'un oscillateur harmonique.
En laboratoire on étudie un dispositif solide-ressort. Dans le référentiel du laboratoire, l'une des extrémités du ressort de raideur k est fixe. L'autre extrémité est reliée à un solide de masse m. La masse oscille autour de sa position d'équilibre avec une période T0 appelée " période propre".
On étudie l'influence de la masse m du solide suspendu au ressort sur sa période propre.

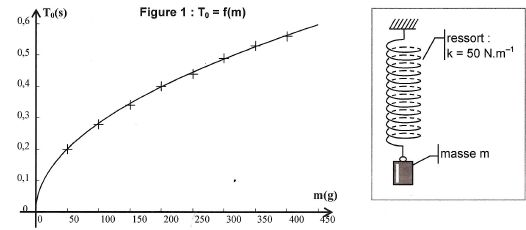La période propre est-elle proportionnelle à la masse du solide ?
La courbe représentant la fonction T0 = f(m) n'est pas une droite : la période propre et la masse m ne sont donc pas proportionnelles.  Par contre on remarque que la période croît avec la masse.
.
.

 


On étudie l'influence de la constante de raideur k du ressort sur la période propre. On utilise un solide de masse m = 0,500 kg.

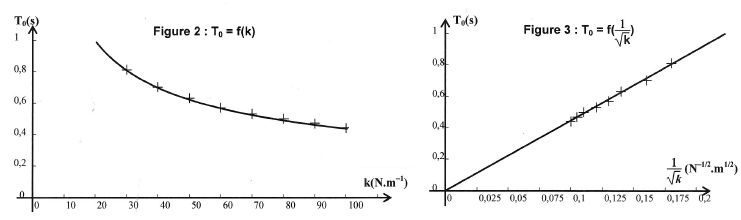
 La période propre est-elle proportionnelle à la constante de raideur k ? Justifier.
La courbe représentant la foncction T0 = f(k) n'est pas une droite : la période propre et la constante de raideur ne sont pas proportionnelles.
La courbe représentant la foncction T0 = f(1 /k½) est  une droite : la période propre et 1 /k½ sont  proportionnelles.
Parmi les expressions suivantes, une seule est cohérente avec les observations expérimentales.

Déterminer laquelle en expliquant le raisonnement.
La première est fausse : elle indique une proportionnalité entre T0 et m ainsi qu'entre T0 et k.
La seconde est fausse : elle indique une proportionnalité entre T0 et 1/ k.
La quatrième est fausse : elle indique que la période décroît avec la masse m.
 T0 = 2p(m/k)½ est cohérente avec les expériences.

.
Spectre infrarouge.
On assimile la liaison  covalente O-H à un oscillateur harmonique de raideur k = 7,2 102 N m-1 et de masse réduite mr.
Un oscillateur lié, à chaque extrémité, à des masses mA et mB est équivalent à un oscillateur dont une extrémité est fixe et dont la masse mr, dite masse réduite, fixée à l'extrémité mobile est :
mr =mA mB / (mA+mB).
Exprimer mr en fonction de m(O), masse d'un atome d'oxygène et m(H) masse d'un atome d'hydrogène.
mr = m(O) m(H) / (m(O) + m(H) ).
En déduire que mr = M(O) M(H) / [(M(O) +M(H)) NA]. Calculer la valeur de mr.
M(H) = 1,0 g/mol ; M(O) = 16,0 g/mol ; NA = 6,02 1023 mol-1.
m(O) = M(O) / NA ; m(H) = M(H) / NA ; m(O) m(H) = M(O) M(H)/ NA2 ; m(O) + m(H) = (M(O) + M(H))/ NA ;
mr = M(O) M(H) / [(M(O) +M(H)) NA].
mr = 1,0 10-3*16,0 10-3 / [(17,0+1,0) 10-3 *6,02 1023 ] =1,563 10-27 ~1,56 10-27 kg.
Montrer que la fréquence propre associée à cet oscillateur harmonique  vaut f0 = 1,1 1014 Hz.
f0 = 1/T0 = 1 / (2p) (k/mr)½ =1/6,28 ( 7,2 102 /(1,563 10-27 ))½ =1,08 1014 ~1,1 1014 Hz.
En calculant la longueur d'onde dans le vide associée à f0 et en supposant que le modèle précédent s'applique à la molécule d'eau, préciser à l'aide du document suivant s'il s'agit d'une vibration d'élongation ou d'une vibration de déformation.
 La molécule d'eau à l'état de vapeur absorbe du rayonnement, notamment dans l'infrarouge. Elle présente trois modes normaux de vibration, tous dans le domaine infrarouge proche :
un mode de vibration d'élongation( stretching ) symétrique à 3652 cm-1( soit pour une longueur d'onde de 2,74 µm ).
Les deux liaisons s'allongent et se racourcissent simultanément.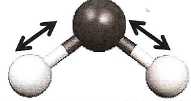
un mode de vibration d'élongation( stretching ) antisymétrique à 3756 cm-1( soit pour une longueur d'onde de 2,66 µm ).
Lorsqu'une liaison s'allonge, l'autre se racourcit et vice-versa..
un mode de vibration de déformation ( dit de cisaillement ) situé à 1595 cm-1 ( soit pour une longueur d'onde de 6,27 µm ).
L'angle entre les liaisons H-O-H oscille.





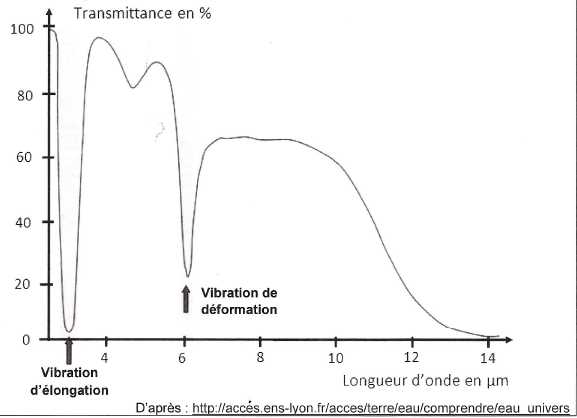
l0 = c / f0 =3,00 108 / (1,08 1014) =2,78 10-6 m = 2,78 µm.
Il s'agit donc d'une vibration d'élongation.



  



menu