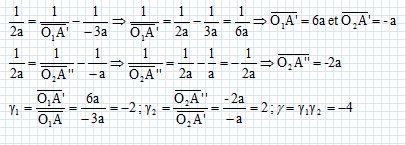Système afocal, lunette astronomique. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

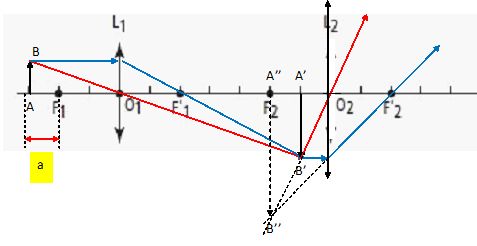
Système afocal. On étudie un système optique constitué de deux lentilles minces convergentes, L1 ( centre optique O1, distance focale image f'1 ) et L2 ( centre optique O2, distance focale image f'2 ). Les lentilles sont utilisées dans les conditions de Gauss. Dans cette première question f'1 = f'2 = 2a et O1O2 = 7 a, la distance "a" étant quelconque. Construire l'image d'un objet réel situé  "3a" à gauche de L1. Déterminer graphiquement le grandissement g. L'objet et l'image définitive sont de sens contraire, le grandissement est négatif : g = -4. Retrouver ces résultats par le calcul. On considère le système optique, appelé lunette, constitué de deux lentilles convergentes de distance focale respective f'1 et f'2. On note D = O1O2, F' : foyer image de la lunette , F : foyer objet de la lunette. Les distances algébriques sont écrites en gras et en bleu. Exprimer O2F' en fonction de f'1, f'2 et D. Un rayon incident parallèle à l'axe optique émerge en passant par le foyer image F'. F' est l'image de F'1 donnée par L2. La relation de Newton ( origine aux foyers) s'écrit : 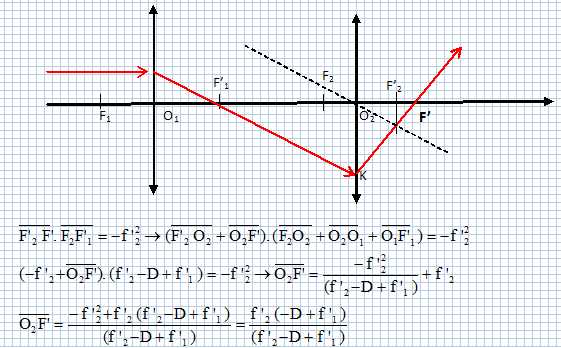Exprimer O1F en fonction de f'1, f'2 et D. Un rayon émergent parallèle à l'axe optique principal, passe par le foyer objet F du système. F2 est l'image de F donnée par L1. La relation de Newton ( origine aux foyers) s'écrit : 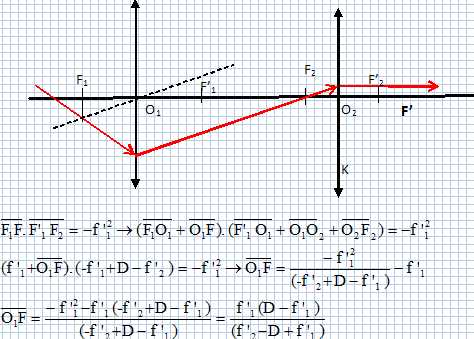Pour quelle valeur de D les foyers sont-ils rejetés à l'infini ? On dit alors que l'association des eux lentilles constitue un système afocal. Le dénominateur des expressions précédentes doit tendre vers zéro : D tend vers f '1 + f '2. 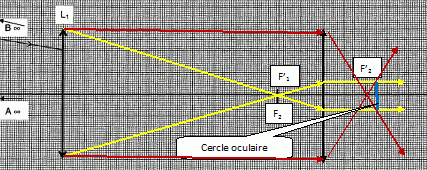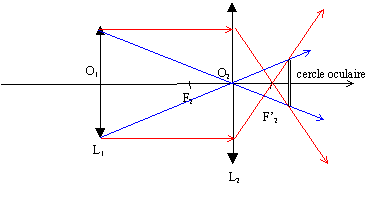Lunette astronomique. On étudie un système optique constitué de deux lentilles minces convergentes, L1 (objectif : centre optique O1, distance focale image f '1 ) et L2 ( oculaire : centre optique O2, distance focale image f '2 ). La lunette permet à un observateur, dont la vue est sans défaut, d'observer sans fatigue un objet à l'infini. On prendra f '1 =6 f '2. Expliquer pourquoi le foyer image de l'objectif doit être confondu avec le foyer objet de l'oculaire. En déduire la distance entre les deux lentilles en fonction de f '2. L'oeil normal observe sans fatigue une image, notée A1B1, située à l'infini. L'objet, noté A2B2 se trouve donc dans le plan focal objet de l'oculaire. A1B1 joue le rôle d'image pour l'objectif ; l'objet, noté AB, étant à l'infini, A1B1 se trouve au foyer image de l'objectif. Le foyer image de l'objectif et le foyer objet de l'oculaire étant confondu, la distance objectif-oculaire est égale à f '1 +f '2 = 6 f '2+f '2 =7 f '2. Tracer la marche d'un faisceau parallèle venant de l'infini et faisant un angle q avec l'axe optique de la lunette. 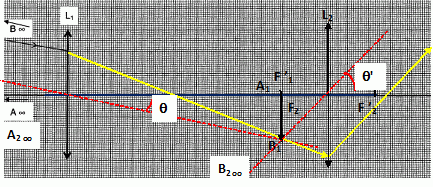Exprimer le grossissement G = q'/q en fonction des distances focales des deux lentilles. tan q = A1B1 / f'1 ~ q ( exprimé en radian ) si l'angle est petit. tan q' = A1B1 / f'2 ~ q' ( exprimé en radian ) si l'angle est petit. tan q =A1B1 / f'1 ~q ; tan q' =A1B1 / f'2 ~q' G = q' / q =f'1 / f'2. .. ..  Définir le cercle oculaire. Construire le cercle oculaire. Le cercle oculaire est l'image de la monture de l'objectif donnée par l'oculaire.   Pourquoi est-il indiqué de placer l'oeil à cet endroit ? Toute la lumière qui entre dans l'instrument d'optique, pénètre dans l'oeil. Soit C le centre du cercle oculaire. Exprimer la distance algébrique O2C en fonction de f '2.  La distance O1O2 vaut f '1+f '2 =7 f '2. Ecrire la formule de conjugaison ( lentille L2) pour calculer O2C.

menu