|
.
|
|
Le
tritium 31H est radioactif ß-, sa
demi-vie est de 12,3 ans.
Qu'est-ce
-qu'un noyau radioactif ?
Un noyau radioactif est un noyau instable dont la
désintégration (destruction) aléatoire s'accompagne :
L'apparition d'un nouveau noyau
L'émission d'une particule notée a, b - ou b
+
L'émission d'un rayonnement électromagnétique noté g.
Définissez
les trois types de radioactivité.
Radioactivité
alpha : un noyau
expulse un noyaux d'hélium.
Radioactivité ß- : un noyau émet un électron noté : -10e. Un neutron du noyau se transforme en proton
Radioactivité ß+ : un
noyau émet un positon noté : +10e. Un proton du noyau se transforme en neutron.
Ecriver l'équation
de la désintégration du noyau de tritium en rappelant les lois utilisées.
31H ---> AZX+
-10e.
Conservation de la charge : 1=
Z-1 d'où Z = 2.
Conservation du nombre de nucléons : 3=A+0.
31H
---> 32He+ -10e.
Quelle est la
signification du terme demi-vie ?
Au bout d'une durée égale à une
demi-vie, l'activité initiale est divisée par deux.
A un instant t0 pris comme origine des temps, le nombre de
noyaux de tritium vaut N0 ;
Donner l'expression
du nombre N de noyaux à l'instant t, en fonction de la demi-vie.
N= N0 exp(-l t)
avec l = ln2 / t½.
ln (N0/N) = lt = ln2
t/ t½ = ln 2t/ t½.
N0/N = 2t/ t½ ; N = N0 / 2t/ t½.
Décollage
vertical d'une fusée.
Représenter
les forces exercées sur la fusée.
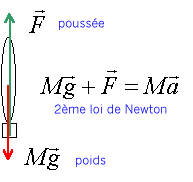
Donner
l'expression de l'accélération dèqs que la fusée a quitté le sol en
négligeant les forces de frottement et en admettant que la masse de la
fusée est constante.
Ecrire la seconde loi de Newton sur un axe vertical ascendant : a = F /
M -g.
Déterminer
l'éqution horaire de la vitesse v(t) de la fusée et celle de sa
position y(t) en admettant que l'accélération est constante.
La vitesse est une primitive de l'accélération ; la vitesse initiale
étant nulle, la constante d'intégration est nulle :
v(t) = at = (F/M-g)t.
La position est une primitive de la vitesse ; la position initiale
étant choisie comme origine de l'axe vertical, la constante
d'intégration est nulle.
y(t) = ½at2 = ½(F/M-g)t2.
Calculer
la distance parcourue par la fusée à t = 6 s.
M = 6,0 105 kg ; F = 1,20 107 N ; g = 10 m s-2.
y = 0,5 ( 1,20 107 /(6,0 105) -10) *62
=1,8 102 m.
|
| .
. |
.
Pendule.
Un pendule simple est
écarté de sa position d'équilibre d'un angle q = 60 °. L'objet suspendu est
assimilable à un objet ponctuel de masse m = 200 g. La longueur du fil
est L = 1,6 m.
Calculer
l'énergie potentielle du système.
Le plan horizontal contenant l'objet en position d'équilibre sera
choisi come plan de référence de l'énergie potentielle de pesanteur.
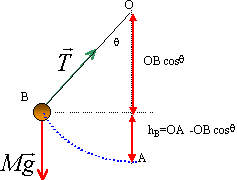
Epp = mg hB = mgL(1-cosq).
Epp =0,200 * 10 *1,6 (1-cos60) =1,6 J.
Calculer
la vitesse du pendule au passage à la position d'équilibre.
La conservation de l'énergie mécanique conduit à : Epp = ½mv2
;
v = (2Epp/ m)½ = (2*1,6/ 0,200)½
= 4,0 m s-1.
|
Cuve à ondes.
On utilise une cuve à ondes dont la pointe frappe la surface de l'eau à la fréquence f = 20 Hz.
Grâce à la stroboscopie, on immobilise le phénomène observé sur le
verre dépoli de la cuve ; on voit alors des cercles clairs et des
cercles noirs. La distance d séparant, sur un rayon, le cercle noir de
rang n et le cercle noir de rang n+4 est mesurée à 18 cm.
Comment qualifie-t-on l'onde obtenue ?
Il s'agit d'ondes mécaniques circulaires transversales.
Calculer la longueur d'onde l des ondes se propageant à la surface de l'eau, le grandissement g du système optique qui fournit l'image sur le verre dépoli étant de 2,25.
La distance d correspond à 4 longueurs d'onde : 4 l g = d ; l = d/ (4g) =18/(4*2,25) = 18 / 9 = 2,0 cm.
Calculer la célérité des ondes.
v = l f = 0,020 * 20 = 0,40 m/s.
|
|

