Influence d'un condensateur et d'une bobine dans un circuit d'allumage de lampes, concours Manipulateur radio  Toulouse 2011.

. .

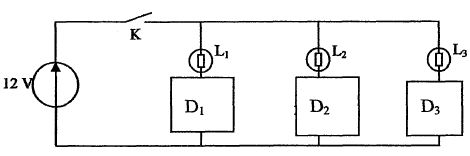
. Un élève dispose de trois dipôles D1, D2, D3 : un conducteur ohmique ( résistance R ), une bobine ( inductance L ) et un condensateur ( capacité C ). Ils ne comportent aucun signe distinctif permettant de les différencier. Pour nommer chaque dipôle, il réalise le montage suivant : Il ferme l'interrupteur et il observe : - La lampe 1, associée avec D1, s'allume instantanément puis reste allumée. - La lampe 2, associée avec D2, s'allume instantanément puis s'éteind progressivement. - La lampe 3, associée avec D3, s'allume seulement après un certain temps puis reste allumée. Pour comprendre ces observations, il étudie les comportements d'un dipôle RC et d'un dipôle RL. Etude du dipôle RC. On réalise un circuit électrique en montant en série une pile de fem E et de résistance interne r, et un condensateur de capacité C = 330 µF. A l'aide d'un dispositif d'acquisition, on enregistre les variations de la tension uc aux bornes du condensateur. On obtient les variations de la charge portée par l'armature A. Vérifier que l'équation différentielle qui régit l'évolution de la charge q = qA portée par l'armature A est : rC dqA/dt +qA = CE. Tension aux bornes du générateur u= uc = E-ri. uc = qA/C et i = dqA/dt. qA/C = E - rdqA/dt ; rC dqA/dt +qA = CE. (1). Vérifier que la solution q(t) = CE(1-exp (-t / t)) est bien solution de l'équation différentielle précédente. dq/dt = CE / t exp (-t / t) ; repport dans (1) : rC CE / t exp (-t / t)+ CE(1-exp (-t / t)) = CE. rC / t exp (-t / t) + 1-exp (-t / t) = 1. Cette égalité est vérifiée quel que soit le temps si t = rC. Donner l'expression de t et vérifier que t est bien homogène à un temps. [r] = V A-1 ; une capacité est une charge divisée par une tension et une charge est une intensité fois un temps. [C] = A T V-1 ; par suite [rC] = T. Quelle est la valeur de la tension aux bornes du condensateur en fin de charge ? en déduire la fem E de la pile. qfin = 4,0 10-3 = CE = C uc fin ; uc fin = E = qfin / C = 4,0 10-3 / (330 10-6) = 12,12 ~12 V. Que vaut le courant i au bout d'un temps suffisamment long ? En courant continu, un condensateur chargé, se comporte comme un interrupteur ouvert : l'intensité est nulle au bout d'un temps suffisamment long. . . . 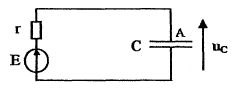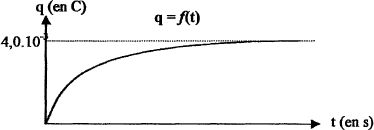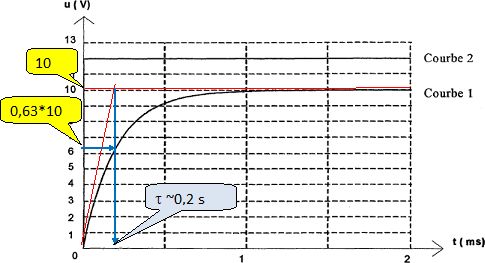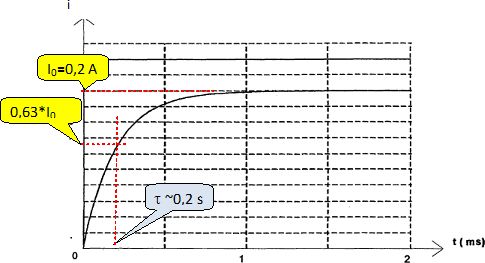Etude du dipôle RL. A l'instant t=0 on ferme l'interrupteur du circuit ci-dessous : 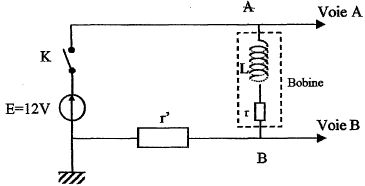Avec un système d'acquisition on enregistre la tension aux bornes de la bobine ( bobine et conducteur ohmique R = r + r' ) sur la voie A et la tension aux bornes du conducteur ohmique de résistance r'= 50,0 ohms sur la voie B. La représentation de uAM et uBM en fonction du temps donne les courbes ci-dessous : Identifier les courbes. 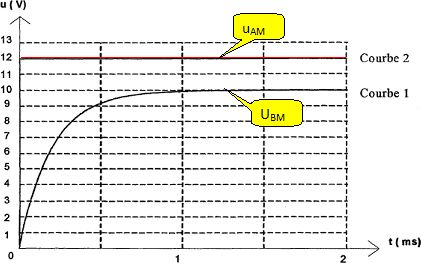Etablir l'équation différentielle régissant l'évolution de i au cours du temps. Additivité des tensions : E = r i + r' i + Ldi/dt = R i + Ldi/dt. Donner l'expression du courant I0 en régime permanent. L'intensité du courant étant constante LdI0/dt = 0 et I0 = E/R. Donner l'expression de t et déterminer  graphiquement sa valeur. Déterminer graphiquement I0. En régime permaent uBM = r' I0 = 10 V ; I0 =10 / 50 = 0,20 A.  Représenter l'allure de la courbe i=f(t) en tenant compte de i à t=0, à t = t et à t très grand. Expliquer comment, graphiquement, calculer la valeur de r. Calculer r, connaissant I0. 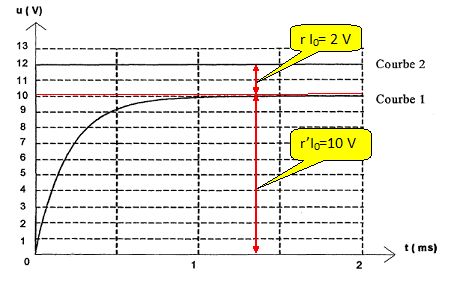r = 2 / 0,2 = 10 ohms. Justifier le comportement des lampes. - La lampe 1, associée avec D1, s'allume instantanément puis reste allumée : D1 est un conducteur ohmique. - La lampe 2, associée avec D2, s'allume instantanément puis s'éteind progressivement : D2 est un condensateur, l'intensité est maximale à t = 0 puis décroît jusqu'à s'annuler. - La lampe 3, associée avec D3, s'allume seulement après un certain temps puis reste allumée : D3 est une bobine, l'intensité est nulle à t = 0 puis croît jusqu'à 0,2 A.

menu