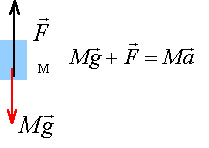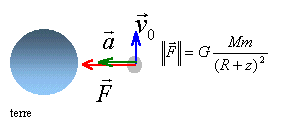|
|
Le vol est constitué de différentes phases.
Phase 1 : lancement.
Le lancement débute lors de
la mise à feu des moteurs et des propulseurs à
poudre. Pendant la phase de décollage on admet que
l'éjection des gaz par les moteurs a les mêmes
effets qu'une force extérieure de valeur F= 32,4
106 N appelée poussée. On suppose
que la valeur de g reste constante durant toute la phase de
départ.
Faire le bilan des forces s'exerçant sur la
navette à l'instant du décollage et
représenter les forces sur un schéma. (au
moment du décollage on néglige les forces
de frottements et la variation de masse).
Système : fusée et équipement;
référentiel terrestre galiléen.
Ecrire la seconde loi de Newton, le système
étant soumis à son poids, à la
poussée des moteurs. Projeter cette relation vectorielle sur un axe vertical
vers le haut.
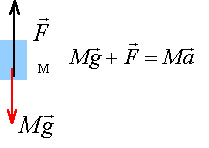
Calculer la valeur de l'accélération au
décollage.
F-Mg= Ma d'où
a = F/M
-g.
a= 32,4 106 / 2,041
106 -9,8 = 15,87-9,8
= 6,06
m/s².
Calculer la distance parcourue pendant les 10 s qui
suivent le décollage en négligeant la
variation d'accélération pendant cette
durée.
Mouvement rectiligne
uniformément accéléré, sans
vitesse initiale :
d= ½ at² =
0,5*6,06*10² = 3,0 102
m.
Phase 2 : vol orbital.
Dix minutes après le
décollage, la navette est en mouvement circulaire
uniforme autour de la terre à l'altitude h= 296 km.
Sa masse est égale à 69,68 103
kg. Son mouvement autour de la terre est circulaire uniforme. L'intensité du champ de gravitation à l'altitude h est gh=6,95 m s-2. Le rayon de la terre est R =6380 km.
Calculer la vitesse du centre d'inertie de la navette.
La navette est soumise à la seule force de
gravitation centripète.
L'accélération est centripète
égal au champ de gravitation à l'altitude
considérée.
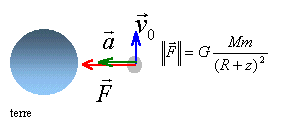
Au sol : g0 = GMterre / R²
d'où GMterre =g0R²
à l'altitude h : gh =
GMterre / (R+h)² = g0R² /
(R+h)².
gh = 9,8 *(6,38 106)² / (6,38
106+ 2,96 105
)²=8,95
m/s².
L'accélération est centripète;
ellest égale à v² / (R+h).
gh = v² / (R+h) ; v² = gh (R+h).
v² = 8,95*(6,38 106+ 2,96 105
)= 59,75 106m²/s².
v = 7,7 103 m / s.
|