|
.
|
|
Alarme
d'appartement.
Après avoir mis sous tension l'alarme d'un
appartement, il faut pouvoir disposer d'une durée suffisante pour
sortir sans la déclencher. Pour cela certains dispositifs utilisent la
charge et la décharge d'un condensateur. Le circuit est alimenté par
une batterie d'accumulateurs de force électromotrice (f.e.m.) E. Le
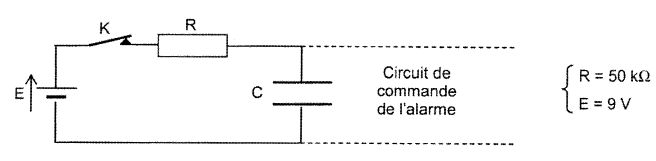
schéma simplifié de l'alarme est le suivant.
La mise sous
tension de l'alarme correspond à la fermeture de l'interrupteur (K). Le
circuit de commande de la sirène est tel qu'à la fermeture de la porte
de l'appartement, le condensateur est mis en court-circuit (ses
armatures sont alors reliées par un fil conducteur non représenté sur
le schéma).
Si la porte n'est pas fermée,
l'alarme se déclenche dès que la tension aux bornes du condensateur
atteint 8 V. A la fermeture de la porte, le condensateur est mis en
court-circuit par un fil conducteur entre les deux armatures.
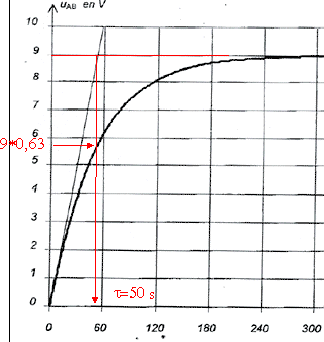
Les variations de la tension uc aux bornes du condensateur à
la fermeture de l'interrupteur K, porte ouverte, sont représentées
ci-dessous :
Déterminer
graphiquement la constante de temps t
du circuit et en déduire la valeur de la capacité du condensateur.
t = RC ; C = t / R = 50 / (50 103) =
1,0 10-3 F.
|
| .
. |
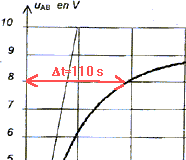
Déterminer la durée D t dont dispose
l'habitant pour quitter l'appartement et fermer la porte, en indiquant
clairement cette durée sur le graphe.
Calculer
l'énergie emmagasinnée par le condensateur durant cet intervalle de
temps.
½Cuc2=0,5 * 1,0 10-3* 82
=3,2 10-2 J.
Etude d'un
circuit RC.
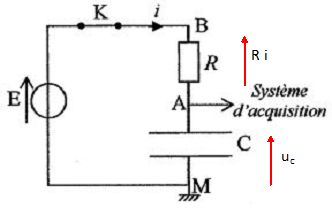
Un
générateur de tension constante E = 5,0 V alimente un conducteur
ohmique de résistance R = 1,0 103 ohms et un condensateur de
capacité C associés en série. Un dispositif d'acquisition de données
relié à un ordinateur permet de suivre l'évolution de la tension aux
bornes du condensateur en fonction du temps. A la date t=0, le
condensateur est initialement déchargé, on ferme l'interrupteur K et
l'ordinateur enregistre la tension dont l'évolution est donnée :
Etablir
l'équation différentielle vérifiée par la tension uc en fléchant les
tensions utilisées.
Additivité des tensions : Ri + uc = E
avec i = dq/dt = C duc/dt.
RC duc/dt + uc = E.
La solution de cette équation différentielle est
du type uc(t) = E(1-exp(-t / (RC)).
Déterminer
graphiquement la constante de temps t
du circuit.( Expliquer la méthode utilisée ).
( Ne possédant pas l'annexe 1, ceci
n'est pas la courbe originale )
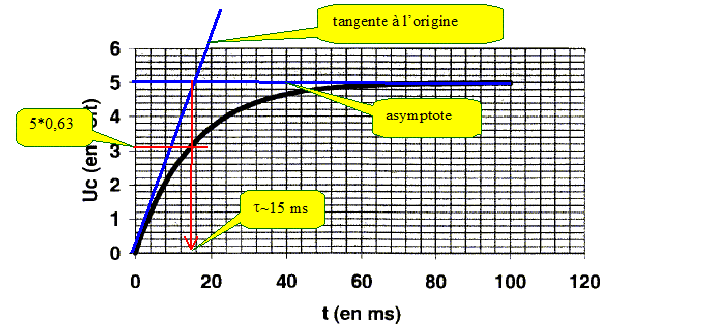
En déduire la
capacité C.
t = RC ; C = t / R = 15 10-3 / (1,0
103) = 1,5 10-5 F.
|
A partir de
l'expression de uc(t), montrer que le courant i(t) durant la
charge peut se mettre sous la forme i(t) = A exp(-kt). On exprimera A
et k en fonction des paramètres.
uc(t) = E(1-exp(-t / (RC)) ; duc/dt
= E / (RC) exp(-t / (RC)).
i(t) = dq/dt = Cduc/dt =E / R exp(-t / (RC)).
On identifie A à E/R et k à 1/(RC).
Que
vaut l'intensité en régime permanent ? décrire le phénomène physique
expliquant cette valeur.
Au bout d'un temps suffisamment long le condensateur est chargé :
l'intensité du courant est nulle. En courant continu, un condensateur
chargé se comporte comme un interrupteur ouvert.
Analogie entre
deux phénomènes.
Loi de croissance radioactive : N(t) = N0 exp(-l t).
Intensité du courant de charge d'un condensateur : i(t) = E / R exp(-t / (RC)).
En
déduire l'équivalent de la constante radioactive l pour le circuit RC.
l est équivalent
à k = 1/(RC) ; tous deux sont l'inverse d'un temps.
Par
analogie avec l'équation différentielle régissant N(t), trouver
l'équation différentielle vérifiée par i(t) au cours de la charge.
dN(t) /dt + l N(t) = 0 ;
di(t) / dt + 1/(RC) i(t) = 0.
|
|




