|
.
|
|
Champ
électromagnétique.
On considère une bobine longue de longueur L = 0,40 m, constituée de
spires jointives et traversée par un courant d'intensité I = 2,0 A.
A) La topographie du champ à l'intérieur de la bobine est le même que
celui d'un aimant droit. (faux) .
A
l'intérieur de la bobine le champ est uniforme ; les lignes de champ
sont parallèles, sauf aux extrémités.
B) Les lignes de champ rentrent par la face nord et sortent par la face
sud de la bobine. (faux).
Les lignes
de champ rentrent par la face sud.
C) Sur les bords de la bobine les
lignes de champ sont parallèles à l'axe de la bobine. ( faux).
D) Si la bobine comprend N = 200 spires, la valeur du champ magnétique
créé au centre de la bobine est B = 1,3 mT. (vrai
).
B = 4 p 10-7 NI / L = 4*3,14 10-7
*200 *2 / 0,40 = 1,3 mT.
La valeur de ce
champ est du mêmeordre de grandeur que celui du champ magnétique
terrestre. ( faux)
Bterre = 2 10-5 T ; B/Bterre ~ 1,3 10-3
/ 2 10-5 ~65.
Conducteur
ohmique.
On dispose de 4 conducteurs ohmiques identiques de résistance R = 47
ohms, d'un générateur de tension idéal de fem E = 8,0 V. L'intensité
débitée par le générateur est I = 0,17 A.
A) La caractéristique courant-tension du générateur est modélisable par
une fonction afine décroissante. ( faux ).
Générateur
idéal de tension, donc la tension aux bornes est constante, égale à E.
B) Les résistors sont associés en série. (faux).
Réquivalente = E/I = 8,0 / 0,17 = 47 ohms.
Pour une
association série, on devrait trouver une résistance équivalente de
4*47 = 188 ohms.
L'association
doit être mixte deux groupes de deux résistors en série, montés en
parallèle aux bornes du générateur.
C) L'énergie dissipée par effet Joule est la même dans tous les dipôles
résistifs. (vrai
).
RI2t,
résistors identiques traversés par la même intensité.
D) La tension aux bornes de chaque résistor
est égale à 4 V. (vrai
).
E) Aucune réponse exacte.
Pendules
électrostatiques.
Deux pendules électrostatiques P1 et P2,
de masse et de longueur identiques portent respectivement les charges q1
et q2 avec |q1| = 3 |q2|
et se positionnent selon le schéma suivant :
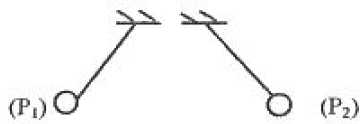
A) La force électrostatique exercée par P1 sur P2
est trois fois plus intense que celle exercée par P2
sur P1. (faux).
Les forces
sont opposées, même direction, sens contraire, même valeur. ( principe
des actions mutuelles).
B) Les deux pendules portent des charges de signe contraire. (faux).
Il y a
répulsion : les charges portées par les pendules sont de même signe.
C) L'interaction électrostatique entre les deux pendules diminue si on
les éloigne l'un de l'autre. (vrai
).
D) La force
électrostatique est proportionnelle à l'inverse de la distance entre
les deux pendules. (faux).
...proportionnelle
à l'inverse du carré de la distance...
E) Il n'existe pas d'interaction gravitationnelle entre les deux
pendules. ( faux).
Les pendules
ont une masse.
|
| .
. |
Charge
d'un condensateur.
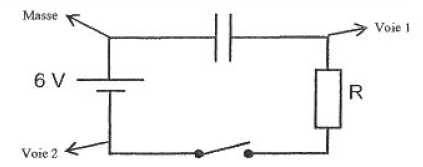
R = 1,0 kW ; C = 0,1 µF. Le
condensateur est initialement déchargé.
A) On peut considérer que la charge est terminée à t = 0,5 ms. (vrai).
RC = 1000 * 10-7
=10-4 s = 0,1 ms. La charge est pratiquement
terminée au bout d'une durée égale à 5 RC.
B) Le système d'acquisition permet de visualiser l'allure de
l'intensité du courant de charge et la tension aux bornes du
condensateur. (faux).
Voie 1, on visualise la tension
aux bornes du condensateur ; voie 2 : on visualise la tension aux
bornes du générateur.
Il faudrait visualiser la
tension aux bornes du résistor.
C)
L'équation qui régit la tension uR aux bornes du conducteur
ohmique pendant la charge est duR/dt + uR/(RC) =
0. (vrai).
Additivité des tensions : E = uR + uC
avec q = C uC ; uR = Ri ; i = dq/dt = uR /
R.
dE/dt = duR/dt +duC/dt ; 0 = duR/dt +1/ C dq /dt ; par suite : duR/dt + uR/(RC) = 0.
D) Lorsqu'on ouvre l'interupteur à t = 5 s, l'intensité du courant dans
le circuit décroît progressivement. (faux).
L'intensité du courant est
nulle dès que le condensateur est chargé.
E) Aucune proposition n'est juste.
Circuit
RC.
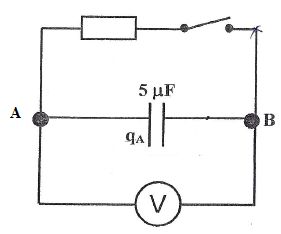
Initialement, le voltmètre
indique U = 5 V et sa borne COM est reliée au point A. L'interrupteur
est ouvert.
A)
L'armature A du condensateur porte une charge qA positive.
(faux).
U = UBA
= qB / C. U et C étant positives, qB
est positive et qA = - qB
est négative.
B) La tension UAB est positive. (faux).
C) L'énergie stockée dans le condensateur vaut environ 62 µJ. (vrai).
½CU2
=0,5 * 5 10-6 *52 =62,5 10-6
J = 62,5 µJ.
D) Le condensateur ne possède aucune énergie.
E) Il existe une tension non nulle aux bornes de l'interrupteur ouvert. (vrai).
L'intensité du courant est
nulle ; la tension aux bornes de l'interrupteur ouvert vaut U = 5 V.
On étudie le circuit après
fermeture de l'interrupteur.
A) Un courant électrique circule dans le conducteur ohmique de A vers
B. (faux).
L'armature A porte une charge négative ;
les électrons se déplace de A vers B à travers le résistor. Le sens
conventionnel du courant est de B vers A à travers le conducteur ohmique.
B) Aucun courant ne circule dans le circuit. ( faux).
C) L'intensité du courant qui circule dans le circuit est constante.
(faux).
L'intensité décroît rapidement
et s'annule.
D) La tension UAB est décroissante et finit par s'annuler.
(faux).
UAB
est initialement négative, elle croît jusqu'à zéro.
E) L'énergie du condensateur est transférée au conducteur ohmique. (vrai ).
Retard
à l'allumage.
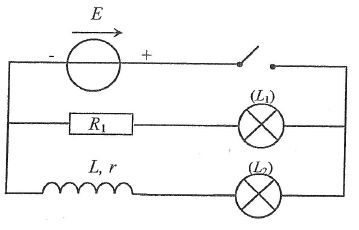
E = 5 V ; R1=r = 10 ohms ; L1 et L2
sont deux lampes identiques. On ferme l'interrupteur à t = 0.
A)
La lampe L1 brille quasi instantanément, la lampe L2
brille avec un retard par rapport à L1. (vrai ).
B) En régime permanent les deux lampes brillent de
façon identique. (vrai
).
En régime permanent , la bobine
se comporte comme un conducteur ohmique de résistance r.
C) En régime permanent aucun courant ne circule dans la branche
contenant le générateur. ( faux).
D) En régime permanent, l'intensité du courant circulant dans R1
est égale à la moitié de l'intensité du courant circulant dans la
branche du générateur. (vrai
).
Intensité dans R1
: E / (R1 + Rlampe) ; intensité du
courant dans la bobine E / (r +
Rlampe) = E / (R1 + Rlampe) ; les intensités des courants dérivés
indentiques s'ajoutent.
E) La tension aux bornes de la bobine augmente pour atteindre une
valeur constante. (faux).
u = Ldi/dt + r i ; initialement i = 0 et u = Ldi/dt = E ; finalement
Ldi/dt = 0 et u = ri avec i =E
/ (r + Rlampe) ; u = E r / (r
+ Rlampe).
La tension aux bornes de la
bobine diminue pour atteindre une valeur constante.
|
Circuit RL.
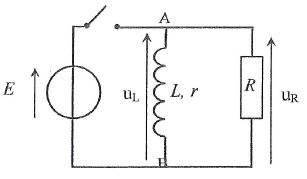
E = 5 V ; R = 1000 ohms ; r = 10 ohms ; L = 50 mH. L'interrupteur est fermé et le régime permanent est établi.
A) L'intensité du courant dans la bobine vaut E/r. (vrai
).
B) L'intensité du courant dans le conducteur ohmique vaut E/R. (vrai
).
C) L'intensité du courant dans le conducteur ohmique est nulle. (faux).
D) L'intensité du courant dans la bobine est nulle. (faux).
E) E = uL + uR.(faux). Circuits dérivés E = uL = uR.
On ouvre l'interrupteur. L'intensité du courant circulant dans le
circuit a pour expression : i = A exp (-Bt), A et B étant constants.
A) L'intensité du courant dans la bobine subit une discontinuité lors de l'ouverture de l'interrupteur. (faux). Continuité de l'énergie stockée par la bobine.
B) Juste après l'ouverture de l'interrupteur, la tension aux bornes de la bobine vaut -500 V. (vrai
).
uL = L [di/dt ]0+ ri(t=0) = L (-AB) exp(0) + E.
En régime permanent, i = E/r = 5/10 = 0,5 A = A exp(0) d'où A = 0,5 A.
1/B est la constante de temps d'un dipole RL ; B =(R+r) / L= 1010 / 0,050 =2,02 104 s-1.
uL = 0,05 (-0,5 *2,02 104 ) + 5 = -500 V.
C) Juste après l'ouverture de l'interrupteur, la tension aux bornes de la bobine est nulle. (faux).
D) Le courant circule de A vers B dans la bobine.(vrai
).
E) L'intensité du courant peut être considérée comme nulle à t = 250 ms. (vrai
).
Constante de temps : L / (R+r) = 0,05 / 1010 ~5 10-5 s = 0,05 ms. L'intensité est nulle au delà de 5 fois la constante de temps.
|
Circuit LC.
L = 0,1 H ; C = 0,1 µF. Le condensateur a été chargé au préalable sous une tension de 6 V. La résistance est négligeable.
A) La période des oscillations libres vaut 10-4 s. ( faux ).
T = 2 p (LC)½ = = 6,28 (0,1*10-7)½ ~6,3 10-4 s.
B) La période des oscillations libres vaut 6,3 10-4 ms. ( faux ).
C) L'énergie totale emmagasinée dans le circuit décroît au cours du temps. ( faux ).
La résistance étant négligeable, l'énergie totale est constante.
D) L'énergie totale emmagasinée dans le circuit est constant et vaut 1,8 10-6 J.(vrai
).
Initialement le condensateur chargé stocke l'énergie totale ½CU2 = 0,5 *10-7 *36 =1,8 10-6 J.
E) L'équation vérifiée par la tension u aux bornes du condensateur est u + 1/(LC) d2u/dt2 = 0. ( faux )
Additivité des tensions : u + Ldi/dt = 0 ; i = dq/dt = Cdu/dt ; di/dt = Cd2u/dt2 ; u + LC d2u/dt2 =0.
|