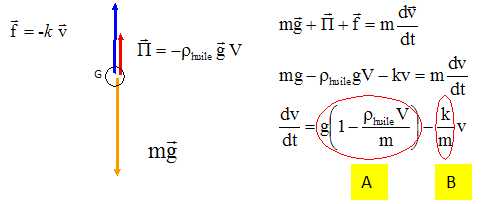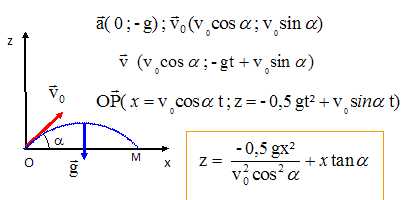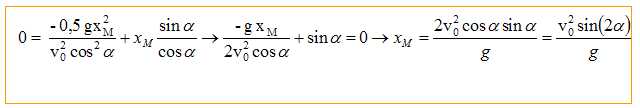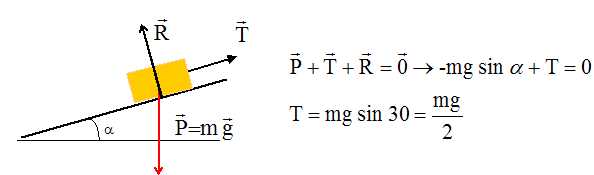|
Mécanique : chute, interactions, ressort, travail, satellite : concours kiné St Michel 2012. |
||||||||
| .
. |
||||||||
|
||||||||
|
Choisir
la ou les réponse(s) exacte(s).
Mécanique
: chute verticale. Dans
un repère Oz vertical, orienté vers le bas, l'équation différentielle
vérifiée par la vitesse de la bille est de la forme : dv/dt = A -B v. D)
Par la méthode d'Euler, en choisissant un pas de calcul Dt = 20 ms, on a
: Mécanique
: chute libre. A) Le vecteur
vitesse initiale étant dans le plan ( xOz ), l'équation du mouvement a
pour expression : B) La balle
atteint le sol pour t1 = 2,0 s. ( vrai ).
.
Mécanique : interactions. On considère deux protons p1 et p2 en contact dans le noyau d'un atome de chlore 35. Soit u un vecteur unitaire de direction ( p1, p2 ) et orienté de p1 vers p2. Aide au calcul : k/G ~1020 ; e / mp ~ 108. A) La force d'interaction gravitationnelle exercée par le proton 1 sur le proton 2 a pour expression : 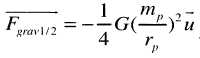 vrai. vrai.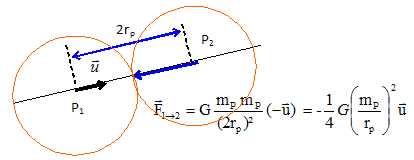 B) La force d'interaction électrique exercée par le proton 2 sur le proton 1 a pour expression : 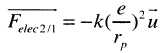 . Faux. . Faux.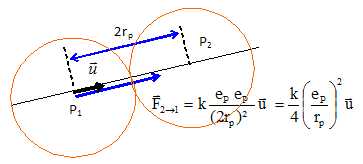 C) Le rapport Fgrav / Félec est de l'ordre de 10-28. Faux. Fgrav / Félec = G / k (mp/ep )2 ~10-20 *10-16 ~10-36. D) La cohésion du noyau est assurée par l'interaction gravitationnelle qui est attractive. Faux. La cohésion du noyau est assurée par l'interaction forte ; la gavitation est négligeable dans l'infiniment petit. Ressort horizontal. On considère un dispositif solide - ressort horizontal. Le ressort a pour raideur k et la période propre du système est notée T0. A) Deux dispositifs solide-ressort sont construits avec deux ressorts de même raideur. Celui qui a le solide de plus petite masse a une période propre plus grande. Faux. T0 = 2p(m/k)½. B) Lorsque le dispositif solide-ressort passe par sa position d'équilibre, la force de rappel est nulle. Vrai. C) Lorsque le dispositif solide-ressort passe par sa position d'équilibre, l'accélération du solide est maximale. Faux. a = - w2x(t) avec x(t) = 0 à la position d'équilibre. D) En absence de frottement, l'abscisse x(t) d'un point du solide vérifie l'équation différentielle : d2x/dt2 + 4p2/T02 x(t) = 0. Vrai. Il faudrait préciser l'abscisse du centre d'inertie du solide.
|
||||||||
|
|
||||||||