Etude de l'allumage d'une voiture : concours manipulateur d'électroradiologie médicale : St Germain.

. .

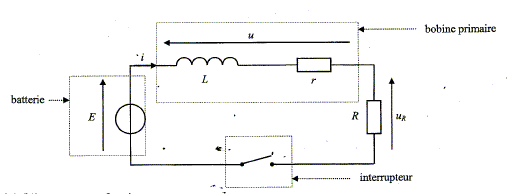
. Pour permettre l'allumage des bougies d'une voiture, une étincelle est créée au niveau des bougies. La formation de cette étincelle est liée à l'ouverture, puis à la fermeture d'un circuit comprenant notamment une bobine. Un courant électrique circule dans un circuit comprenant la batterie de la voiture, la bobine appelée bobine primaire et un interrupteur électronique. On considérera que la batterie de la voiture délivre une tension continue qui vaut E = 12 V. La bobine primaire est caractérisée par une inductance L et une résistance interne r = 0,50 W. Le schéma simplifié du principe est donné ci-dessous où R représente la résistance des autres éléments du circuit. On prendra R = 2,5W. A t = 0, le courant ne circule pas dans le circuit, puis l'interrupteur est fermé. Donner l'expression de la tension u aux bornes de la bobine primaire en fonction de r, L et i. u = Ldi/dt + r i. Montrer que l'équation différentielle régissant l'évolution de i est: : L di/dt +Ki = E où K est une constante dont on donnera l'expression en fonction des paramètres du circuit. additivité des tensions : u + uR= E avec uR= Ri d'où Ldi/dt + (R+r) i = E (1). Expression de la forme Ldi/dt + K i= E avec K= R+r exprimée en ohm. Une solution de l'équation différentielle peut s'écrire i =A (1- exp(-Bt)) où A et B sont deux constantes positives non nulles. En utilisant l'équation différentielle, montrer que A = E/K et que B = K/L. - Calculer la valeur de A. Préciser son unité. Dériver i(t) par rapport au temps : di/dt = ABexp(-Bt). Repport dans (1) : ABLexp(-Bt) +AK-AKexp(-Bt) = E Cette égalité est vérifiée quel que soit le temps si : BL=K soit B=K/L et si AK= E soit A= E/K. Calcul de la valeur de A : A = E/(R+r) avec E=12 V et R+r =3W. A = 12/3 = 4 ampères. . . . 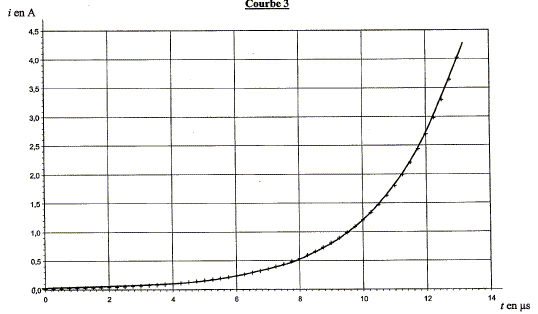Parmi les courbes 1, 2 et 3 données ci-dessous, indiquer, en justifiant, celle qui peut représenter i. 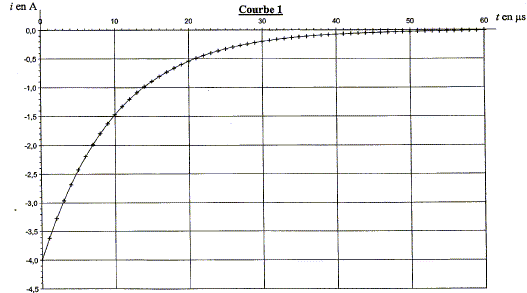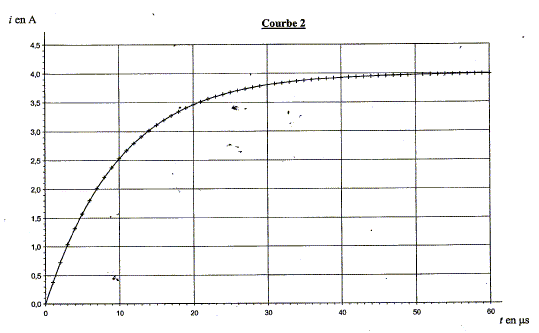La courbe 2 correspond à l'intensité i(t) =4 (1- exp(-Bt)) La courbe correspond à une fonction croissante de la valeur 0 à la valeur 4 A en accord avec l'expression de i(t) proposée. Donner l'expression littérale de la constante de temps t en fonction des paramètres du circuit. t = L/(R+r).

menu