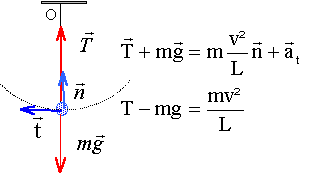|
|
Un oscillateur
est constitué par un solide de masse m, attaché à l'extrémité d'un
ressort à spires non jointives, de masse négligeable et de
constante de raideur k. Le solide oscille sans frottement selon un axe
horizontal. On repère la position, à l'instant t, du centre d'inertie G
de S par l'abscisse x. L'origine O du repère correspond à la position
du centre d'inertie G de S à l'équilibre. Le graphe ci-dessous donne
les variations de l'énergie cinétique du centre G du solide S en
fonction de l'abscisse x. On donne m = 100 g ; g = 10 SI.
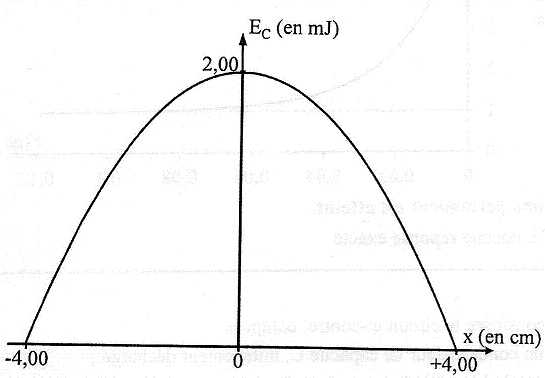
Calculer la période propre T0 en seconde de
l'oscillateur.
( 0,63 ; 1,26 ; 1,50 ; 1,76 ; 2,52 ; aucune réponse exacte ).
La
conservation de l'énergie mécanique du système solide ressort
conduit à :
½k X2max = ½mv2max = 2,00 10-3.
½k *0,0402 =
2,00 10-3.
k = 4,00
10-3 / (4 10-2)2 =10 / 4 = 2,5 N m-1.
T0 = 2 p (m/k)½ = 6,28 (0,1 / 2,5)½ =6,28 *0,04½ =6,28*0,2 =1,26 s.
Un
pendule simple est constitué d'un solide ponctuel de masse m. Ce solide
est attaché à l'extrémité d'un fil inextensible, de masse négligeable
et de longueur L. On écarte le pendule simple ainsi constitué d'un
angle q0
de sa position d'équilibre et on le lâche sans vitesse initiale. On
négligera tous les frottements.
Parmi les expressions suivantes, laquelle donne la valeur de la tension
du fil, au passage de la position d'équilibre.
A) mg (2 + 3 cos q0)
; B) mg (3 + 2 cos q0)
; C) mg
(3 - 2 cos q0)
; D ) mg
(1 - 3 cos q0)
; E) mg
(1+ cos q0)
;
F) autre expression.
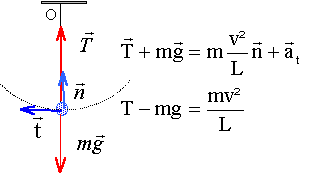
Conservation de l'énergie mécanique :
½mv2max =mg
L(1-cos q0).
v2max
=2g L(1-cos q0).
Au passage à la position d'équilibre : l'accélération vaut : a
= a = v2max
/ L =2g(1-cos q0).
La seconde loi de Newton s'écrit sur un axe vertical ascendant :
-mg + T = ma = 2mg(1-cos q0).
T = 2mg(1-cos q0) +
mg = mg ( 3-2 cos q0).
|