Durée : 20 min. Il n'y a pas de points
négatfs ; une question peut comporter plusieurs réponses dans ce cas,
un demi-point est accordé si une et une seule réponse exacte est
manquante.
|
|
Une bille en
chute libre de masse m = 100 g est lancée vers le haut avec une vitesse
initiale v0 = 5 m/s. On a relevé l'altitude de la bille à
intervalles réguliers. La courbe de l'énergie potentielle de pesanteur,
le sol est choisi comme référence, ainsi que la courbe de l'énergie
cinétique en fonction du temps ont été représentées ci-dessous. ( g =
10 SI et 6½~2,5). La bille a été lancée d'une altitude h et
retombe sur le sol avec une vitesse d'environ :
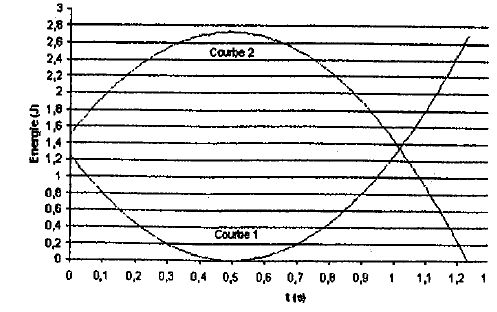
A) h = 0 m ;
v = 5 m/s.
B) h = 1,45 m ; v = 7,5 m/s..
C) h = 1,25 m ; v = 7,5 m/s.
D) h = 2,7 m ; v = 5 m/s.
E) h = 1,45 m ; v = 5 m/s.
F) Aucune proposition exacte.
La chute étant libre,
l'énergie mécanique se conserve :
Iniitalement, cett énergie vaut : mgh + ½mv02.
Finalement, au sol, l'énergie mécanique vaut ½mv2.
Par suite : ½mv2 = mgh + ½mv02.
v2 =2gh + v02 ;
v = (2gh + v02)½.
Si
h = 0, v = v0 mais h=0 contredit le graphique. A)
est faux.
Si h = 1,45, v = (20*1,45 + 25)½ =54½ = (9*6)½
~3,2,5 = 7,5 m/s : B) est vrai. C) D) et E) sont
faux.
|
| .
. |
.
A et B se
rendent au cours de physique de la prépa par le métro.
P se trouve entre les stations S1 et S2 distantes
de 1 km en ligne droite, plus précisément à 550 m de S1 et à
450 m de S2.
A et B empruntent la même rame de métro, mais A descend à la station S1
et B à la station suivante S2. Entre chaque station, le
métro démarre avec une accélération constante a = 1 m s-2
jusqu'à atteindre la vitesse de 36 km/h qu'il conserve pendant un
certain temps, puis il décélère avec l'accélération constante a' = 1 m s-2
jusqu'à l'arrêt.
Dès que A et B sortent du métro, ils marchent à la vitesse constante de
6 km/h.
A) Le métro parcourt la
distance entre S1 et S2 en 1 min 50 s. Vrai.
Phase accélérée : d1
= ½at2 ; vfin = at ; t =(36/3,6) / 1 = 10 s et d1
= 0,5*1*102 = 50 m.
Lors du freinage, la distance parcourue est la même et la durée du
ralentissement est 10 s.
Le métro parcourt donc 900 m à la vitesse constante de 6 m/s :
durée correspondante : 900/10 = 90 s. Durée totale : 110 s = 1 min 50 .
B) B arrive à P avant A. Faux.
A parcourt 550 m en :
550 /( 6/3,6 )=550*0,6 = 330 s.
B parcout 450 m en 450 /(
6/3,6 )=450*0,6 = 270 s.
Durée totale du trajet de B depuis la station S1 :270+110 =
380 s.
C) B arrive à P 6min 20 s
après avoir quitté la station S1. Vrai.
380 s = 6 min 20 s.
D) B et A arrivent à P avec 50 s
d'intervalle.Vrai.
380-330 = 50 s.
E) Le métro roule à
vitesse constante sur 900 m. Vrai.
F) Aucune proposition n'est exacte. Faux.
Une
balle de petite dimensions, dont la densité vaut les deux-tiers de celle
de l'eau, est maintenue au fond d'un récipient horizontal
contenant une hauteur d'eau de 40 cm. On néglige les frottementss
et g = 10 SI . La balle est libérée sans vitesse initiale.
Sa vitesse en arrivant à la surface de l'eau est ( en m/s) : A) 2 *2½ ; B) 8½ ; C) 2.
On note V : volume de la balle ; µ : masse volumique de l'eau.
La
balle est soumise à son poids, vertical, vers le bas, valeur P = mg = V
2/3µg et à la poussée d'Archimède, verticale, vers le haut, valeur : F
= V µ g.
La seconde loi de Newton s'écrit sur un axe vertical, orienté vers le haut, origine le fond du récipient :
V µ g- V 2/3µg = V 2/3µ dv/dt ; dv/dt = 0,5 g ; v(t) = 0,5 gt ; x(t) = 0,25 gt2 = v2(t) / g ; v(t) = (g x(t))½ = (10*0,4)½ = 2 m/s. C) est donc vrai.
Quittant la surface de l'eau, on considère que la balle n'est soumise qu'à son poids.
La hauteur maximale atteinte par la balle au dessus de la surface du liquide est en cm : D) 20 ; E) 40 ; F) 10.
L'énergie mécanique se conserve ; la surface de l'eau est prise comme origine de l'énergie potentielle de pesanteur.
Au départ cette énergie vaut : ½mv2 .
Au point le plus haut, la
vitesse est nulle et l'énergie mécanique se trouve sous forme d'énergie
potentielle à l'altitude h : mgh.
Par suite : mgh = ½mv2 ; h = v2/(2g) = 4 /20 = 0,20 m = 20 cm. (D) est donc vrai).
|
|
