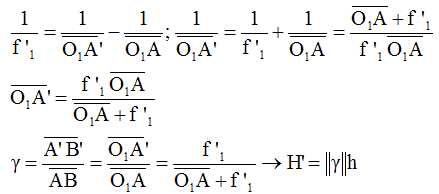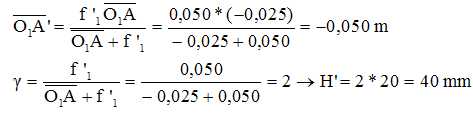|
.
|
|
On
considère deux lentilles minces. La première notée L1
de distance focale image f'1= 50 mm et la deuxième
notée L2 de distance focale image f'2= -
50 mm.
Indiquer
le moyen le plus simple possible de les distinguer.
Au toucher la lentille L1 a le centre plus épais
que les bords ; sa vergence est positive: elle est convergente.
La lentille L2 a les bords plus épais que la
partie centrale ; sa vergence est
négative: elle est divergente.
(2).
On considère pour chacune de ces lentilles le même objet réel noté AB,
tel que AB =
20 mm. Cet
objet est placé à 25 mm de la lentille.
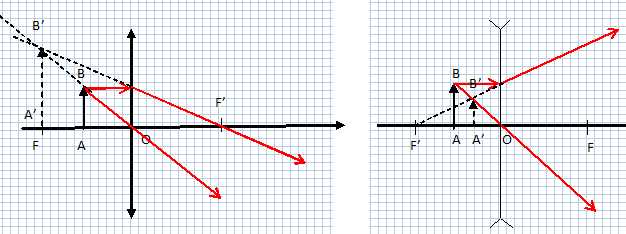
Construire
f image que donne chacune des deux lentilles de cet objet
(on fera deux constructions
diffèrentes, en utilisant verticalement et horizontalement une échelle
1).
Indiquer
sans justification les caractéristiques des deux images précédentes.
Les deux images sont virtuelles et droites. L1
donne une image plus grande, L2 une image plus
petite.
On
considère maintenant la lentille L1 seule. Un
objet réel AB de hauteur h est situé à une distance d du
centre optique de la lentille.
Donner
sans justification, les expressions littérales de mesure algébrique de O1A', g et H', respectivement
position, grandissement
et
hauteur de l' image A'B' de l'objet précédent au travers de la lentille.
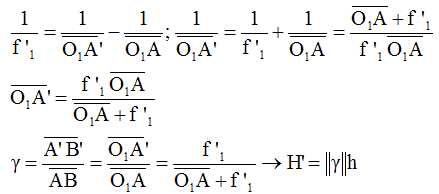
Dans
le cas du (2) et pour la lentille L1, vérifier
par calcul numérique 1es caractéristiques trouvées
pour l'image. Justifier.
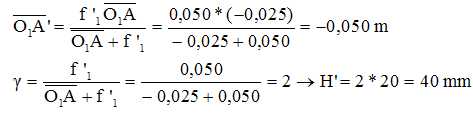
|
| .
. |
.
Un
photographe fait un reportage sportif lors du 100 m des jeux
olynpiques. Il veut photographier un sprinter qui se déplace
perpendiculairement à l'axe optique à une distance D=20 m. Le coureur
a pour hauteur H=1,80 m et le format de la pellicule est de (18 x 24)
mm.
Le
temps de pose pour prendre la photo doit-il être grand ou petit ?
Pourquoi ?
Le temps de pose doit être petit car le sprinter est en mouvement ; si
le temps de pose est trop grand, l'image sera floue.
On considère chacun des objectifs comme une lentille
mince. Le photographe dispose de 3 objectifs de focales 50 mm ; 135 mm
et 300 mm.
Comment
peut-on considérer le sprinter par rapport à l'objectif ? En déduire où
va alors se former son image? Justifier.
La distance entre l'objectif et le sprinter est très supérieure à la
distance focale : l'objet est considéré à l'infini et son image est
dans le plan focal image de l'objectif.
En
déduire l'expression littérale de la taille de l'image obtenue sur la
pellicule (on suppose la mise au point effectuée
convenablement).
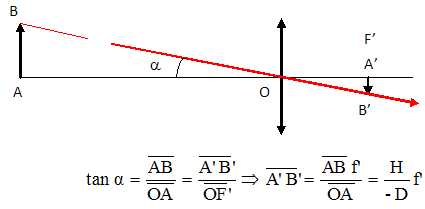
(2 c). Calculer
la taille de l'image dans les 3 cas et en déduire quel objectif il doit
choisir pour que l' image du coureur soit la plus grande possible mais
qu'elle soit toute entière sur la pellicule.
hauteur de l'image : h' =1,80 / 20 f' = 0,09 f'.
h'1 = 0,09*50 =4,5 mm ; h'2
= 0,09*135 ~12 mm ; h'3
= 0,09*300 ~27
mm, valeur supérieure à la taiile de la pellicule.
L'objectif de focale 135 mm convient.
Le photographe
choisit un temps de pose , t
=1/250 s et un nombre d'ouverture N=5,0.
Calculer
le diamètre de la pupille d'entrée DPE, en
prenant pour f' la valeur trouvée en 2) c).
Indication
: la pupille d'entrée d'un objectif photographique est un trou
circulaire, son diamètre et la focale sont liés par la formule f ' =
N DPE .
DPE = f' / N =
135/5,0 = 27 mm.
Il
est possible
de changer le temps de pose t
et le nombre d'ouverture N, mais il faut que l'énergie lumineuse E
reçue par la pellicule reste constante.
Cette énergie est proportionnelle au temps de pose t et à la
surface S de la pupille d'entrée. Soit k le coefficient de
proportionnalité.
Écrire
(sans justification) la relation littérale entre l'énergie E reçue par
la pellicule, le temps de pose t et la
surface S de la pupille d'entrée.
E = k t S
avec S = pDPE2/4.
En
déduire (sans justification) la relation littérale entre l'énergie E
reçue par la pellicule, le temps de pose
t,
f' et le nombre d'ouverture N.
E = k t pDPE2/4
= k t p(f'/N)2/4.
Calculer
le nombre d'ouverture N' correspondant à un temps de pose t'= 1,0 ms.
k t p(f'/N)2/4
= k t' p(f'/N')2/4.
t /N2
= t' /N'2
d'où N' = N(t' /t )½
=5,0 ( 1,0 / 4,0)½ =2,5.
|
|