|
Répondre
aux questions en expliquant brièvement votre démarche.
|
|
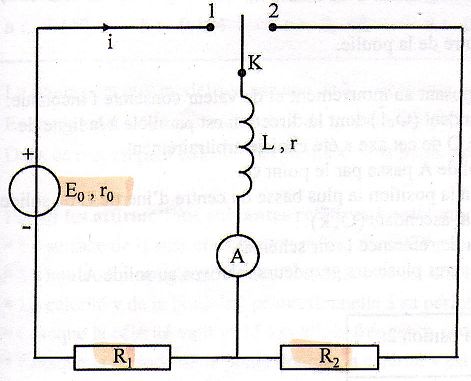
Le
circuit ci-dessous comporte :
- Un générateur de tension de fem E0 et de
résistance interne r0.
- un interrupteur K à deux positions.
- Une bobine d'inductance L et de résistance r.
- Deux conducteurs ohmiques de résistances R1 et
R2.
- Un ampèremètre.
La
bobine sera considérée comme un solénoïde de longueur L, de diamètre D
et comportant N spires.
E0 = 12 V ; r0 = 2,0 ohms
; R1 = 20 ohms ; R2 = 7,0
ohms ; L
= 52 cm ; D = 9,0 cm.
L'inductance du solénoïde est L = µ0N2S/l où S
désigne la surface d'une spire.
La valeur du champ magnétique à l'intérieur du solénoïde est : B0
=µ0N I / l.
On place
l'interrupteur en position 1 pendant le temps nécessaire pour atteindre
le régime permanent.
On place la sonde d'un teslamètre à l'intérieur de la bobine et on
mesure la valeur du champ magnétique B0 = 1,8 mT.
L'ampèremètre indique I = 0,48 A.
|
| .
. |
.
Déterminer
la valeur de l'inductance L ( en mH) de la bobine.
S =pD2/4
=3,14 *0,092/4 =6,362 10-3
m2.
B0
=µ0N I / l ; N = B0 l
/(µ0
I) =1,8 10-3 *0,52 /( *3,14 10-7
*0,48) =1,552 103.
L = µ0N2S/l=4 *3,14 10-7*(1,552 103)2 *6,362 10-3
/ 0,52=3,7
10-2 T = 37 mH.
Calculer
la valeur de la résistance r de la bobine.
En
régime permanent la bobine se comporte comme un conducteur ohmique : la
tension à ses bornes est r I.
Additivité des tensions : E0-r0I
= R1I +rI ; r = E0/I-r0-R1
= 12/0,48-2-20= 3,0 ohms.
En
déduire la valeur ELmax ( en mJ) de l'énergie
stockée dans la bobine en régime permanent.
ELmax = ½LI2 =0,5
*0,037*0,482 =4,26 10-3 J
~4,3
mJ.
A un
instant t=0 pris comme origine des dates, on bascule l'interrupteur en
position 2. L'équation différentielle qui traduit l'évolution de
l'intensité du courant dans le circuit est di/dt +i/t=0.
Pour résoudre numériquement cette équation, on utilisera exclusivement
la méthode itérative d'Euler. On prendra un pas de calcul Dt égal au dixième
de la valeur de la constante de temps du circuit.
Déterminer
la valeur de l'intensité i ( en A) du courant à a date t = 5 Dt.
t =
L/(R2+r) =0,037 /(7+3) =3,7 10-3
s.
A t=0, r i(0) = E0-(r0+R1)i(0)
; i(0) = E0/(r+r0+R1)=12/(2+3+20)
=0,48 A.
A t0+, la continuité de
l'intensité impose i(t0+)=0,48 A.
Di
= i(t0+Dt)
-i(t0) = -i(t0) Dt/ t =
-0,48*3,7 10-4
/3,7 10-3
=-0,048 A ; i(t0+Dt)= 0,48 -0,048
=0,432 A.
i(t0+2Dt) -i(t0+Dt)
= -i(t0+Dt) Dt/ t =
-0,432*3,7 10-4
/3,7 10-3
=-0,0432 A ; i(t0+2Dt)= 0,432 -0,0432
=0,3888 A.
i(t0+3Dt) -i(t0+2Dt) = -i(t0+2Dt) Dt/ t =
-0,3888*3,7 10-4
/3,7 10-3
=-0,03888 A ; i(t0+3Dt)= 0,3888
-0,03888 =0,345 A.
i(t0+4Dt) -i(t0+3Dt) = -i(t0+3Dt) Dt/ t =
-0,345*3,7 10-4
/3,7 10-3
=-0,0345 A ; i(t0+4Dt)= 0,345 -0,0345
=0,3154 A.
i(t0+5Dt) -i(t0+4Dt) = -i(t0+4Dt) Dt/ t =
-0,3154*3,7 10-4
/3,7 10-3
=-0,03154 A ; i(t0+5Dt)= 0,3154
-0,03154 =0,284 A ~0,28 A.
En
déduire le pourcentage P d'énergie encore stockée dans la bobine à la
date t = 5 Dt.
½LI'2 =0,5*0,037*0,2842
=1,49 10-3 J ~1,5 mJ.
P =1,5 *100 / 4,26 =35,2 ~35 %.
|
|
