|
Choisir
la réponse exacte.
|
|
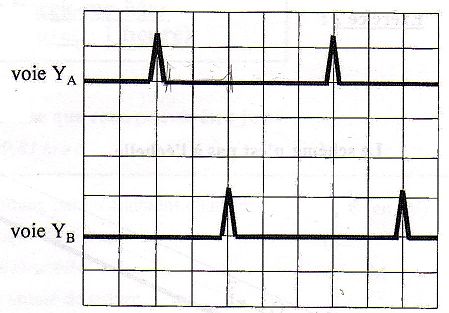
Tube à rayons X.
Dans un tube à rayons X, des électrons sont émis dans le vide, sans
vitesse initiale, par un filament chauffé. Ces électrons sont accélérés
par une tension électrique et vont frapper une plaque de cuivre. On
donne le diagramme simplifié des niveaux d'énergie de l'atome de cuivre.

L'énergie de l'électron incident est suffisante pour arracher un
électron du niveau K de l'atome de cuivre. Cet électron arraché, un
électron de la couche L ou de la couche M peut passer sur la couche K.
Le spectre émis par le tube est composé de deux raies, notées Ka et Kß.
Calculer
( en nm) la valeur de la plus grande longueur d'onde des deux raies
émises.
(0,140 ; 0,154 ; 0,167 ; 0,175 ; 0,187 ; aucune réponse exacte ).
A la
plus grande longueur d'onde correspond la plus petite différence
d'énergie ( transition L --> K ).
l = hc / DE avec DE = 8979-931 =8048 eV ou 8048*1.6 10-19
=1,2877 10-15 J.
l = 6,63 10-34 *3,00 108
/ (1,2877 10-15)= 1,54 10-10
m ~0,154
nm.
La houle.
La houle peut être modélisée par une onde mécanique, périodique,
sinusoïdale, se propageant à la surface de la mer. En haute mer, la
longueur d'onde l de la
houle est petite devant la profondeur de la mer. Dans ce cas, on peut
calculer la célérité de la houle par la relation v = (gl / (2p))½.
Parmi
les affirmations suivantes relatives à cette modélisation de la houle,
combien y en a-t-il d'exactes ?
- La surface de la mer constitue un milieu dispersif pour la houle. Vrai.
l = v / f ; v2
= gl / (2p) = gv / (2pf) ; v = g / (2pf) ; la célérité dépend de la fréquence.
- La houle se propageant à la surface de la mer est une onde
longitudinale. Faux. ( transversale
).
- La célérité v de la houle est proportionnelle à la période. Vrai.
v = g
/ (2pf) = gT / (2p).
- Si la la célérité v vaut 15 km/h, la fréquence f vaut 3,7 Hz. Faux.
15 / 3,6 = 4,17 m/s ; f = g / (2pv)= 9,81 / (6,28*4,17) =0,37 Hz.
- Si la période double, la célérité est divisée par deux. Faux.
Satellite.
Un satellite artificiel S1
de masse m1 =1,35 103 kg gravite en orbite
circulaire autour de la terre à l'altitude h1 = 420 km.Rayon
terrestre RT =6,38 103 km ; MT =5,98 1024
kg.
On considère un deuxième satellite S2 de masse m2 =3,87 103
kg en orbite circulaire autour de la terre à l'altitude h2.
La valeur de la force de gravitation exercée par la terre sur S1
est égale à la valeur de la force de gravitation exercée par la terre
sur S2. Calculer h2 ( en km).
(1,12 103 ; 2,27 103 ; 4,28 103 ; 5,13 103 ; 6,78 103 ;
aurtre réponse ).
GMTm1
/ (RT+h1)2 = GMTm2
/ (RT+h2)2 ; ((RT+h2)/
RT+h1))=
(m2/m1)½= (3,87 /
1,35)½=1,693.
RT+h2
= 1,693*(6380+420) =1,15 104 km ; h2 =5,13 103 km.
|
| .
. |
Pendules simples.
On considère deux pendules simples de longueurs respectives L1
et L2. Ces deux pendules sont écartés de leurs positions
d'équilibre d'un même petit angle a
et lachés sans vitesse initiale. Le rapport des périodes propres des
oscillations non amorties des deux pendules est T1/T2
= 1,5.
Calculer
le rapport w1/w2 des amplitudes des
vitesses angulaires des deux pendules.
( 0,67 ; 1,0 ; 1,5 ; 2,3 ; 3,0 ; autre réponse ).
w1 = 2p/T1 ; w2 = 2p/T2 ; w1/w2
= T2/T1 =1/1,5 = 0,67.
Fission.
Sous l'impact d'un neutron lent,
un noyau de plutonium 24194Pu subit une réaction
de fission. Il se forme alors deux noyaux : du césium 14155Cs
et de l'yttrium 9839Y et plusieurs neutrons sont
libérés.
On donne : m(24194Pu) = 241,00514 u ; m(14155Cs) = 140,79352 u ; m(9839Y) =97,90070 u ; m(neutron)
=1,00866 u ; c = 2,9979 108 m/s ; 1 eV = 1,6022 10-19
J ; 1 u = 1,66054 10-27 kg.
Calculer
l'énergie en MeV libérée lors de cette fission.
(273,5 ; 283,2 ; 289,4 ; 293,1 ; 298,6 ; autre réponse ).
24194Pu+10n
---> 14155Cs +9839Y
+310n
.
|Dm| = |140,79352 +97,90070 +2*1,00866 -241,00514|=0,2936
u ou 0,2936*1,66054 10-27
=4,8753 10-28 kg.
E = |Dm| c2=4,8753 10-28
*(2,9979
108)2 =4,3816 10-11 J ou 4,3816 10-11
/1,6022 10-13
= 273,5
MeV.
Force
de Coulomb.
Deux petites
sphères identiques de masse m = 2,75 g sont accrochées chacune à
l'extrémité inférieure de deux fils inextensibles et de longueur L =
25,0 cm. Ces deux xphères portent la même charge q.. A l'équilibre, les
deux fils sont écartés d'un angle a
par rapport à la verticale. On donne k = 8,99 109 SI.
Calculer
la valeur de q ( en nC).
(48 ; 61 ; 82
; 91 ; 98 ; autre réponse )

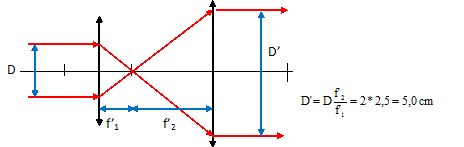
Lentilles.
Un dispositif optique est constitué de deux lentilles minces
convergentes L1 et L2 de distances focales
respectives f'1 = 2,0 cm et f'2 = 5,0 cm. Les
deux axes optiques des lentilles sont confondus et la distance des deux
centres optiques est x = 7,0 cm. Un faisceau cylindrique de lumière de
diamètre D = 2,0 cm est formé de rayons parallèles à l'axe optique. Ce
faisceau traverse la lentille L1, l'axe du cylindre étant
confondu avec l'axe optique.
Calculer
le diamètre D' ( en cm ) du faisceau à la sortie de L2.
(1,0 ; 2,0 ; 3,0 ; 4,0 ; 5,0
).
Courbe d'Aston.
On considère 4
noyaux atomiques X1, X2, X3 et X4
placés sur la courbe d'Aston ci-dessous :
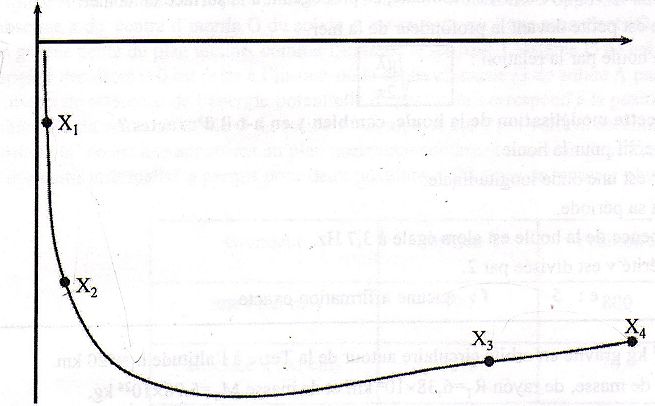
Parmi les
affirmations suivantes, combien y en a-t-il d'exactes ?
- La courbe d'Aston représente l'énergie de liaison par nucléon El/A
en fonction du nombre de nucléons. Faux
( -El/A en fonction du nombre de nucléons)
- Un noyau est d'autant plus stable que son énergie de liaison par nucléon est plus
petite. Faux ( ...plus grande )
- Le noyau X3 est plus stable que le noyau X4. Vrai.
- Le noyau X4 peut subir la fission nucléaire. Vrai.
- X2 peut être un produit de fusion de X1. Vrai.
Dipôle
RC.
On place en série un générateur idéal de tension de fem E, un
interrupteur, un conducteur ohmique de résistance R = 4,7 kW et un condensateur de capacité
C. Le condensateur étant initialement déchargé, on ferme l'interrupteur
à un instant pris comme origine des temps. Un oscilloscope à mémoire a
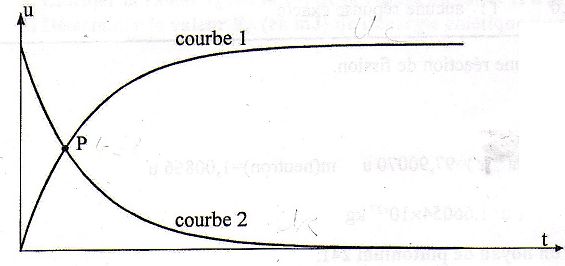
permis d'obtenir les courbes suivantes :
Courbe 1 :
évolution de la tension aux bornes du condensateur en fonction du temps.
Courbe 2 : évolution de la
tension aux bornes du conducteur ohmique en fonction du temps.
Coordonnées du point P ( 12,4 ms ; 6,0 V).
Calculer
la valeur de C ( en µF).(1,2 ; 1,8 ; 2,4 ; 3,2 ; 3,8 ; autre
réponse.
Courbe 1 : uc = E(1-exp(-t / (RC)) ; courbe 2 : uR = E exp(-t/(RC)).
Point P :
E(1-exp(-t / (RC)) =E
exp(-t/(RC)) ;
0,5 =exp(-t/(RC))
ln 2 = 12,4
10-3/(RC) ; RC =12,4
10-3/ln 2 =0,0179 ; C = 0,0179 / (4,7 103)
=3,8
µF.
|
|