Le condensateur.
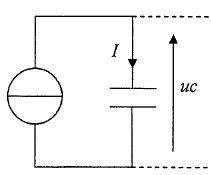
Pour déterminer la capacité C d'un condensateur on utilise le montage
suivant. Le générateur débite un courant constant I= 0,20 mA. Un
dispositif, non représenté, permet d'enregistrer la tension uc
aux bornes du condensateur en fonction du temps et de le décharger dès
que la tension entre ses bornes atteint 12 V. On constatte que la
tension passe de 0 à 12 V en Dt
= 240 ms.
|
|
Rappeler la relation
entre la charge q du condensateur et la tension uc.
q = Cuc.
Etablir la relation entre C, I, Dt et uc. Calculer C.
L'intensité I étant constante, q = I Dt.
I Dt = Cuc ; C = I Dt/ uc = 0,20 10-3 *0,240 /
12 =4,0 10-6 F = 4,0 µF.
La bobine.
Pour déterminer l'inductance L et la résistance r d'une bobine, on
utilise le montage suivant. Le générateur maintient une tension E = 6,0
V entre ses bornes. Un système d'acquisition non représenté, permet
d'enregistrer la tension aux bornes de R1. Un traitement
informatisé permet de tracer la courbe de l'évolution de i en fonction
du temps.
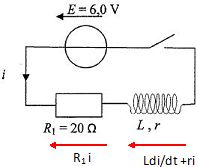
A l'instant t=0 on ferme l'interrupteur.
Etablir l'équation
différentielle que satisfait l'intensité i. On posera Rt
= r +R1.
Additivité des tensions : E = R1 i + Ldi/dt + ri ; E = L
di/dt + Rt i.
Montrer
que la solution i = E/Rt(1-exp(-t/
t)) avec t = L/Rt convient.
Dériver i par rapport au temps : di/dt = E/Rt / t exp(-t/ t)
=E / L exp(-t/ t).
repport dans l'équation différentielle : E = E exp(-t/ t) +Rt
( E/Rt(1-exp(-t/
t)))
E = E exp(-t/ t) +E -E exp(-t/ t) : égalité vérifiée quel que
soit le temps.
|
| .
. |
A
partir de la courbe, déterminer Rt.
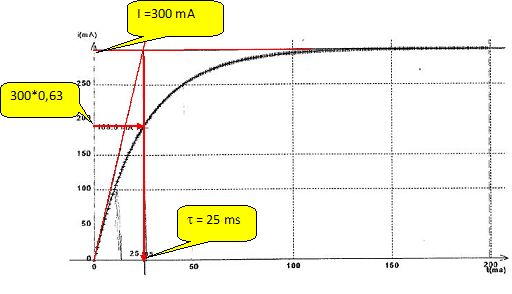
En régime permanent, l'intensité est constante ( I ~ 0,30 A) et dI/dt =
0. Par suite E = Rt I soit Rt = E/I ~ 6/0,3 ~20 ohms.
Or Rt = r +R1.
En
conséquence r est négligeable devant R1.
Déterminer
graphiquement L.
L = t Rt = 25 10-3
*20 = 0,50 H.
Oscillations électriques.
On
réalise le montage suivant. A t = 0 on ferme l'interupteur, le
condensateur ayant été chargé au préalable de sorte que la tension uc soit égale à 5,0 V.
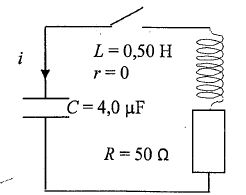
On relève l'évolution de uc en fonction de t. La résistance critique de ce circuit vaut 270 ohms.
Quel est le régime observé ? Déterminer graphiquement la pseudo-période T.
On observe un régime pseudopériodique.
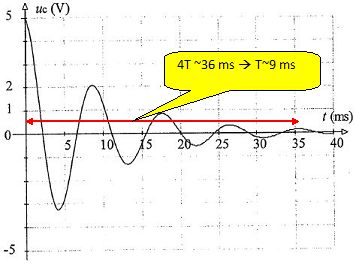
Calculer la période propre T0 du circuit et comparer à T. On donne p 2½ = 4,443.
T0 = 2 p(LC)½ = 2 p(0,5*4 10-6)½ = 2 p 2½ 10-3 =2*4,443 ms =8,886 ~8,9 ms.
Ecart relatif : (9-8,886) / 9 ~ 1 %. A % près, on peut confondre T et T0.
Pour obtenir des oscillations non amorties on ajoute un élément en série dans le circuit.
Comment se nomme un tel dispositif ? Quel est son rôle ?
Un dispositif simulant une résistance négative compense à chaque instant l'énergie perdue par effet joule dans la résistance R.
|
Dans le cas d'oscillations non amorties, la tension uc peut s'écrire uc = 5,0 cos (500 *2½t).
En déduire l'expression de i en fonction du temps.
i = dq/dt = Cduc/dt = -C *5,0*500 *2½sin (500 *2½t).
i(t) =-4 10-6 *5,0*500 *2½sin (500 *2½t) = -1,41 10-2 sin (500 *2½t).
Calculer l'énergie emmagasinée dans le condensateur lors de sa charge préalable.
½CE2 = 0,5 *4 10-6 *52 = 5,0 10-5 J.
Quel est le pourcentage d'énergie électrique dissipée au bout d'une pseudo-période ?
La tension aux bornes du condensateur ne vaut plus que 2V ( lecture
graphe ). Le condenateur stocke toute l'énergie du dipole RLC à t = T
soit : 0,5 *4 10-6 *22 = 8,0 10-6 J.
Energie perdue par effet Joule lors de la première pseudo-période : 5,0 10-5 - 8,0 10-6= 4,2 10-5 J.
4,2 10-5 /5,0 10-5 =0,84 ( 84 % ).
|
|




