On se propose d'étudier la vitesse de la réaction entre les
ions iodure I- et les ions peroxodisulfate S2O82-.
|
|
On prépare 300 mL d'une solution d'iodure de
potassium dont la concentration en soluté dissous KI est
égale à c1 = 2/15 mol/L.
On prépare 300 mL d'une solution de
peroxodisulfate de potassium dont la concentration en
soluté dissous K2S2O8 est
égale à c2 = 1/30 mol/L.
A l'instant t=0 on mélange les deux solutions, on obtient un mélange de
volume V = 600 mL.
Mélange initial
et réaction étudiée.
La réaction étudiée a pour équation : 2I-aq + S2O82-aq
= I2aq + 2SO42-aq.
Ecrire
les deux couples oxydant / réducteur mis en jeu.
S2O82-
aq/ SO42- aq et I2 aq/ I-aq.
Déterminer les quantités de matière
initiales des ions iodure, des ions peroxodisulfate et des ions
ptassium dans le mélange initial.
n(I-aq)0=0,300
*2/15 =4,0 10-2 mol.
n(S2O82-
aq)0=0,300*1/30 = 1,0 10-2 mol.
n(K+ aq)0= 4,0 10-2 + 2,0 10-2 = 6,0
10-2 mol.
Autre méthode
: la solution reste électriquement
neutre :
n(I-aq)0+
2 n(S2O82-
aq)0=n(K+
aq)0.
On observe le mélange : il change de teinte, passant de
l'incolore au jaune de plus en plus foncé, puis au marron.
En
quoi cette observation confirme-t-elle que la réaction est lente
?
L'oeil a le temps de suivre l'évolution de la couleur de la solution et
de distinguer les différentes teintes.
On sait que la réaction est totale.
Construire,
avec les valeurs numériques, un tableau descriptif d'évolution du
système chimique.
|
avancement
(mol)
|
2I-aq |
+ S2O82-aq |
= I2aq |
+ 2SO42-aq. |
initial
|
0
|
0,04
|
0,01
|
0
|
0
|
en
cours
|
x
|
0,04-2x
|
0,01-x
|
x
|
2x
|
fin
|
xmax
|
0,04-2xmax |
0,01-xmax |
xmax |
xmax |
|
| .
. |
Quelle
est la quantité de diiode formée quand la réaction est terminée ?
Si I-aq est en défaut : 0,04-2xmax= 0 ; xmax= = 0,02 mol.
Si S2O82-aq est en défaut : 0,01-xmax= 0 ; xmax= = 0,01 mol. On retient la plus petite valeur (S2O82-aq est en défaut).
Il se forme donc 0,010 mol = 10 mmol de I2aq.
Etude cinétique.
On recommence la même expérience, dans des conditions identiques, mais
cette fois, toutes les cinq minutes, on prélève un volume V0=25,0
mL du mélange ; on lui ajoute approximativement 100 mL d'eau très
froide et un peu d'empois d'amidon. On dose le diiode en solution avec
une solution de thiosulfate de sodium de concentration c3=
0,010 mol/L. L'équation support du titrage est :
I2aq + 2S2O32-aq = 2 I-aq
+ S4O62-aq.
Pourquoi
ajoite-t-on de l'eau froide au prélevement ?
L'ajout d'eau froide réalise un
blocage cinétique de la réaction.
Quelles
sont les caractéristiques indispensables de la réaction pour qu'elle
puisse servir de titrage ?
La réaction doit être rapide et totale.
Dans quoi
place-t-on la solution titrante ? éprouvette graduée,
burette graduée, fiole jaugée, becher, erlenmeyer.
La solution titrante se trouve dans une burette graduée.
Quel est
le rôle de l'empois d'amidon ?
L'empois d'amidon joue le rôle d'indicateur de fin de réaction.
Pour chaque titrage, le volume VE de solution titrante pour
obtenir l'équivalence est donnée dans le tableau ci-dessous.
Justifier
la relation x = 0,12 VE qui a été utilisée
pour compléter la 3è ligne du tableau.
A l'équivalence les quantités de matière des réactifs sont en
proportions stoechiométriques : x = n(I2aq) = ½n(S2O32-aq).
x = ½VE c3 = 0,5 *0,01 VE ; [I2aq]
= 0,005 *0,01 VE mol de diode dans le prélevement de
25 mL soit 0,005*600 / 25 = 0,12 VE dans le
mélange total de volume 600 mL.
| t(min)
|
0
|
5
|
10
|
15
|
20
|
25
|
30
|
35
|
40
|
45
|
50
|
55
|
60
|
65
|
70 |
VE(mL)
|
0
|
1,5
|
2,6
|
3,7
|
4,5
|
6,0
|
6,8
|
7,8
|
8,8
|
9,7
|
10,5
|
11,4
|
12,4
|
13,2
|
13,7
|
x
(mmol)
|
0
|
0,18
|
0,31
|
0,44
|
0,54
|
0,72
|
0,82
|
0,94
|
1,06
|
1,16
|
1,26
|
1,37
|
1,49
|
1,58
|
1,64
|
|
A partir du tableau on a
construit la courbe d'évolution de l'avancement x (mmol) en fonction du
temps (min).
Rappeler
la définition de la vitesse volumique de réaction. Peut-on la
déterminer à t=0 ? Si non indiquer pourquoi et si oui, donner sa valeur.
v = 1/V dx/dt avec V =0,60 L volume de la solution.
dx/dt est le coefficient
directeur de la tangente à la courbe à la date t. On peut donc déterminer graphiquement [dx/dt]t=0
puis en divisant par V = 0,60 L, calculer la vitesse initiale de la
réaction.
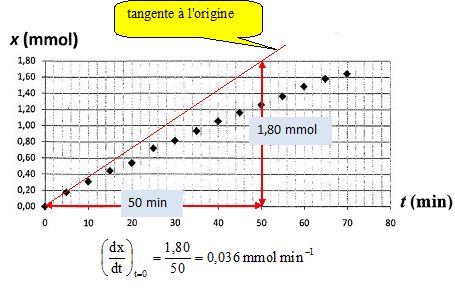
v(t=0) =
0,036 / 0,6 = 0,06 mmol L-1 min-1.
Rappeler la
définition du temps de demi-réaction. Peut-on le déterminer ? Si non
indiquer pourquoi et si oui, donner sa valeur.
Le temps de demi-réaction est la durée au bout
de laquelle l'avancement est égal à la moitié de l'avancement final. La
réaction étant totale xfin = xmax = 0,010 mol.
xt½ = ½xfin = 0,005 mol = 5,0 mmol. Le graphe ne
permet pas la détermination de t½.
|
|
