La grêle se forme dans les cumulo-nimbus situés entre 1 000 m
et 10 000 m d'altitude où la température est très basse, jusqu'à –
40°C. Le grêlon tombe lorsqu'il n'est plus maintenu au sein du nuage.
Au sol sa vitesse peut atteindre 160 km/h.
On étudie un grêlon de masse 13 g qui tombe d'un point O d'altitude 1
500 m sans vitesse initiale. Il peut être assimilé à une sphère de
diamètre 3,0 cm. Le point O sera pris comme origine d'un axe Oz orienté
positivement vers le bas. L'intensité de la pesanteur sera considérée
comme constante et de valeur g0 = 9,80 m.s-2 .
Données : volume d'une sphère V = 4/3 p.r3
; masse volumique de l'air r = 1,3 kg.m-3
.
|
|
A ) Chute libre : on admettra que le grêlon tombe en chute libre.
En
appliquant la deuxième loi de
Newton, déterminer les équations horaires donnant la vitesse et la
position du centre d'inertie G du grêlon en fonction de la durée t de
chute.
On applique la deuxième loi de
Newton au grêlon dans le référentiel terrestre supposé galiléen ; on
choisi un axe vertical orienté vers le bas, origine : le point de
départ O.
En chute libre, le poids est la
seule force appliquée : ma = mg d'où a=g.
La vitesse est une
primitive de l'accélération : v= gt ( la constante d'intégration est
nulle car la vitesse initiale est nulle).
La position est une primitive de la vitesse :
z= ½gt².( position initiale prise comme origine).
Calculer la valeur de la vitesse lorsqu'il
atteint le sol, ce résultat est-il vraisemblable ? Justifier.
au
sol z = 1500 m ; t²= 3000/g ; t = [3000/g]½.
Repport dans l'expression de la vitesse : v = g[3000/g]½ =
[3000*g]½ = [3000*9,8]½ = 171,5 m/s=617 km/h.
Cette valeur est bien trop grande pour correspondre à la réalité ,
ainsi qu'à la valeur proposée dans le texte; on a négligé les forces de
frottements sur les couches d'air.
B ) Chute réelle :
En réalité le grêlon est soumis à deux autres forces, la poussée
d'Archimède FA et la force de frottement fluide F
proportionnelle au carré de la vitesse telle que F = K.v2.
Par une analyse
dimensionnelle, déterminer l'unité du coefficient K dans le Système
International.
F : force ( newton) = Masse *
accélération soit [M][L][T]-2 ;
vitesse ² = longueur ² / temps²
soit [L]2[T]-2 ;
K= F/v² soit [M][L][T]-2 [L]-2[T]2 = [M][L]-1
L'unité du coefficient K dans
le Système International est donc kg.m-1.
Donner
l'expression de la valeur de la poussée d'Archimède; la calculer et la
comparer à celle du poids. Conclure.
Poussée d'Archimède = poids du
volume de fluide (air) déplacé = volume grêlon * rair*g.
FA= 4/3 p.r3 rairg avec r = 1,5 10-2 m.
FA= 4/3*3,14*(1,5 10-2)3*1,3*9,8
= 1,8 10-4 N.
poids P=mg= 0,013*9,8 = 0,13 N
La poussée d'Archimède est négligeable devant le poids du grêlon.
|
| .
. |
.
On néglige la poussée
d'Archimède.
Etablir l'équation différentielle du
mouvement. Montrer qu'elle peut s'écrire sous la
forme dv/dt = A – B.v2.
Ecrire la seconde loi de Newton dans un
référentiel terrestre supposé
galiléen, suivant un axe vertical
descendant.
Le
grêlon est soumis à son poids, vertical vers le
bas et à la force de frottement verticale vers le
haut.
mg -
Kv² = ma = m dv/dt soit dv/dt =
g-K/mv².
A = g et B=
K/m.
On veut résoudre cette équation
différentielle par une méthode
numérique : la méthode d'Euler. Le tableau
suivant est un extrait d'une feuille de calcul des
valeurs de la vitesse (v) et de
l'accélération (a) en fonction du temps
(t). Il correspond aux valeurs : A = 10,0
m.s-2 et B = 1,56.10-2
m-1 , pas de variation Dt
= 0,5 s.
t(s)
|
v(m/s)
|
a(m s-2)
|
0,00
|
0,00
|
10,0
|
0,50
|
5,00
|
a1
|
1,00
|
v2
|
8,46
|
1,50
|
14,03
|
6,85
|
2,00
|
17,46
|
5,12
|
2,50
|
20,02
|
3,59
|
3,00
|
21,81
|
2,39
|
Déterminer a1 et v2 en
détaillant les calculs.
On utilise
l'équation différentielle pour
déterminer a1 :
a1
= 10-1,6 10-2 v12 avec
v1 = 5,00 m/s.
a1
= 10-1,6 10-2* 5,002
= 9,6
m/s².
Dans la
méthode d'Euler, on utilise l'approximation suivante
: a =
Dv /
D
t.
Dv
= v2-v1=
a2D
t soit
v2= v1+
a1D
t.
v2= 5 + 9,6 * 0,5 = 9,8
m/s.
Exprimer la vitesse limite atteinte par le grêlon
en fonction de A et B puis calculer sa valeur
numérique.
Lorsque la
vitesse limite est atteinte par le grêlon, la vitesse
est constante, l'accélération a est alors
nulle.
0=
A-Bvl2 soit vl
=(A/B)½= (9,8/1,56
10-2)½=25,1
m/s.
|
La courbe d'évolution de la vitesse en fonction
du temps est donnée ci-dessous.
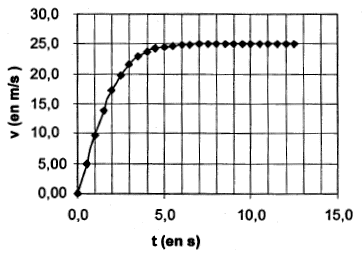
D'après
cette courbe, quelle est la valeur de v2 ? Quelle est la valeur de la
vitesse limite ? Est-ce en accord avec le valeurs déterminées ci-dessus
?
D'après
la courbe, l'asymptote horizontale donne la valeur de la
vitesse limite ( 25 m/s ), valeur en accord avec celle calculée
ci-dessus.
L'ordonnée correspondante à t = 1 s,donne v2 ~10 m/s, valeur en accord avec celle calculée
ci-dessus.
Indiquer le nom des deux régimes observés et évaluer le temps caractéristique de cette chute.
Régime permanent dès que la vitesse limite est atteinte ; auparavant, le régime est transitoire.
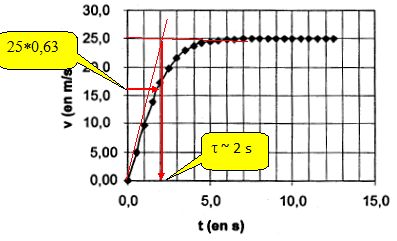
|
|

