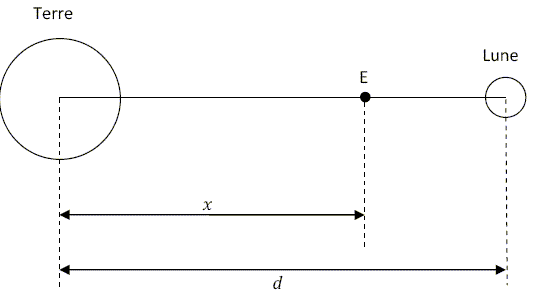
Gravitation, satellite, équigravité terre lune, vitesse de libération : concours Audioprothésiste.

. .

. Données : G = 6,67 10-11 N m2 kg-2 ; Mterre =5,98 1024 kg ; Mlune =7,34 1022 kg ; Rterre =6,37 106 m ; Rlune =1,74 106 m ; distance des surfaces terre-lune D = 3,84 108 m ; durée du jour solaire T1 = 86400 s ; durée du jour sidéral T2 = 86164 s. La terre et la lune sont considérés comme des corps sphériques homogènes. Calculer le champ de gravitation à la surface de la lune. g = G Mlune / R2lune =6,67 10-11 *7,34 1022 / (1,74 106)2= 1,617 ~1,62 m s-2. Calculer la force de gravitation qu'exerce la lune sur la terre. F = G Mterre Mlune / (D +Rterre +Rlune)2. F = 6,67 10-11*5,98 1024 *7,34 1022 / (3,84 108+6,37 106 +1,74 106)2 =1,90 1020 N. Il existe un point E du segment joignant les centres de la terre et de la lune tel que la force de gravitation soit nulle. Calculer la distance du centre de la terre au point E. En E, on considère un objet de masse m = 1 kg. Force exercée par la terre sur l'objet : F =GMT/x2 ; force exercée par la lune sur l'objet : F =GML/(d-x)2 ; GMT/x2 = GML/(d-x)2 ; (MT/ML)½ = x / (d-x). x (1 +(MT/ML)½ = d(MT/ML)½  ; x = d(MT/ML)½  / (1 +(MT/ML)½ ) ; (1 +(MT/ML)½ )= (1 +(5,98 1024 /7,34 1022)½ )=  10,026. d(MT/ML)½ = (3,84 108+6,37 106 +1,74 106)(5,98 1024 /7,34 1022)½  =3,5324 109. x= 3,5324 109 / 10,026 = 3,52 108 m. ( ~0,9 d ). Indiquer le domaine où l'action gravitationnelle de l'un des deux astres est prépondérante. A gauche du point E ( voir figure ci-dessus ) l'action gravitationnelle de la terre est prépondérante. . . Démontrer que l'énergie potentielle de gravitation d'un corps de masse m situé à la distance r du centre d'une planète de masse M vaut Ep = -GMm/r. L'énergie potentielle est nulle à l'infini. Les vecteurs sont écrits en bleu et en gras. La force exercée par la planète sur le satellite en orbite circulaire est une force centrale qui dérive d’une énergie potentielle Ep, ainsi on a : F = -dEp/dr er  où er représente le vecteur unitaire radial et r le rayon de l'orbite ciculaire. Expression vectorielle du champ de force f(r) auquel est soumis le satellite : Le satellite n'est soumis qu'à la force de gravitation attractive exercée par la planète. La direction de cette force passe toujours par le point O, centre de la planète : il s'agit donc d'un champ de forces centrales. f(r) = GMm/r2(-er) Montrons que la force f qui s'exerce sur le satellite S dérive d'une énergie potentielle de gravitation Ep. Le travail de la force f (r) ne dépend que des positions initiale et finale ( peu importe le chemin suivi) : la force est conservative. On peut associer à cette force, une fonction scalaire ou énergie potentielle notée Ep(r), définie à une constante près ; la variation de l'énergie potentielle entre les points A et B est égale à l'opposée du travail de la forcef(r) entre ces points. 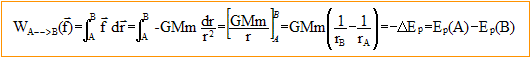En prenant B situé à l'infini ( par convention cette énergie potentielle est nulle à l'infini), il vient : Ep = -GMm/r.  La vitesse de libération vlib correspond à la vitesse initiale minimale que doit avoir un objet situé à une distance d du centre d'un corps très massif de masse M afin de pouvoir s'en éloigner jusquà une distance infinie. Exprimer la vitesse de libération vlib d'un objet situé à la surface d'une planète de masse M et de rayon r en fonction de M et r. Faire l'application numérique pour la terre et la lune. Expression de l'énergie mécanique Esol de ce satellite dans le référentiel géocentrique avant son lancement : l'énergie potentielle vaut Ep= -GMm/R ; l'énergie cinétique communiquée par la Terre vaut : Ec = ½mv2 avec v = 463 m/s. l'énergie mécanique vaut : Esol = -GMm/R + ½mvlib2 L'énergie mécanique à une distance infinie est nulle d'où : ½mvlib2 = GMm/R. vlib2 = 2MG/R ; vlib =[2MG/R]½. Calcul de cette vitesse d’évasion pour un corps quelconque se situant à la surface de la Terre : vlib =[2*5,98 1024*6,67 10-11 / 6,38 106]½=11,2 km/s. Calcul de cette vitesse d’évasion pour un corps quelconque se situant à la surface de la Lune : vlib =[2*7,34 1022*6,67 10-11 / 1,74 106]½=2,37 km/s. Déterminer l'altitude à laquelle doit évoluer un satellite terrestre géostationnaire. 3ème loi de kepler : T2 / z3 = 4p2/(GMT) =4*3,142 /(5,98 1024*6,67 10-11) = 9,9 10-14. z3 = 861642 / 9,9 10-14=7,5 1022 ; z = 4,217 107 m altitude = z-RT =4,217 107 - 6,37 106 =3,58 107 m. Un satellite passe tous les 26 jours à 830 km au dessus de la verticale d'un lieu terrestre après 370 révolutions. Montrer que pour une période ( mesurée à 1 % près) ces données sont compatibles avec le fait qu'il a une trajectoire circulaire autour de la terre. T = 26*24*3600/370=6,07 103 s. v = (GMT/(RT+h))½ =(6,67 10-11 *5,98 1024 /(6,37106+8,3 105))½ =7,44 103 m/s. Circonférence : 2p (RT+h)) = v T. 2*3,14(6,37106+8,3 105) =4,52 107 m ;  vT = 7,44 103*6,07 103 =  4,52 107 m. Les données sont compatibles avec une trajectoire circulaire.

menu