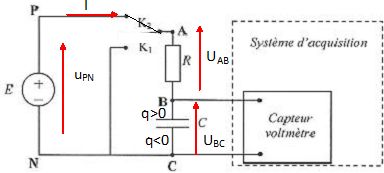
Dipole RC , dipole RLC : concours Audioprothésiste.

. .

. Le montage du circuit comprend : un générateur idéal de tension de fem E, un interrupteur deux positions, un conducteur ohmique de résistance R, un condensateur de capacité C. Représenter sur le schéma les flèches des tensions uPN, uAB et uBC ansi que le courant I et les charges des armatures du condensateur. (voir schéma ci-dessus ) Déterminer l'équation différentielle donnant les variations de la tension uBC en fonction du temps. Additivité des tensions uPN = UBC + uAB ; E = UBC +R I avec I = dq/dt et q = CuBC. I = CduBC/dt d'où : E = UBC +RCduBC/dt duBC/dt + 1/(RC)UBC = E/ (RC). Déterminer graphiquement E et la constante de temps du circuit t = RC. . . Donner l'unité de t par analyse dimensionnelle. 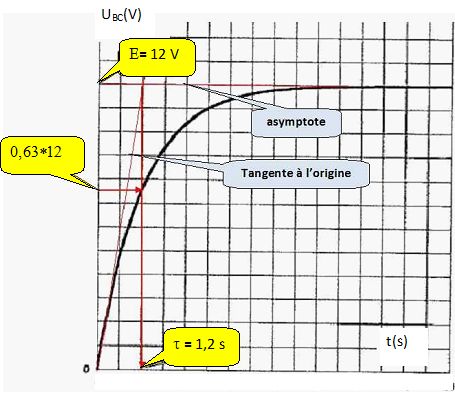Tension aux bornes d'un conducteur ohmique U = R I d'où R = U / I : V A-1. Charge d'une armature du condensateur Q =C U = I t si I est constant soit C = It / U : A s V-1. RC s'exprime donc en  seconde. Calculer C si R = 1000 ohms. C = t / R = 1,2 / 1000 = 1,2 10-3 F. En déduire l'énergie stockée par le condensateur chargé. Energie = ½CE2 =0,5 *1,2 10-3 *122 =8,6 10-2 J. Décrire le phénomène qui se produit lorsqu'on bascule l'interrupteur en position K1. La constante t change-t-elle ? Si oui, pourquoi ? On observe la décharge du condensateur à travers le conducteur ohmique R. La résistance du circuit ne change pas, alors la constante de temps reste inchangée. Une fois le condensateur chargé, on remplace R par une bobine d'inductance L et de résistance r, puis on bascule l'interrupteur en position K1. 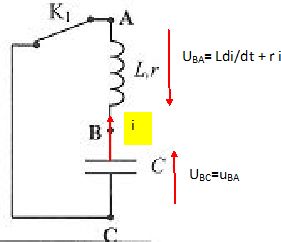Déterminer l'équation différentielle donnant les variations de la tension uBC. uBC = Ldi/dt + ri avec i = -dq/dt = -CduBC/dt et di/dt = -C d2uBC/dt2. uBC = -LCd2uBC/dt2 - r C di/dt. LCd2uBC/dt2 + r C di/dt  + uBC =0. On suppose qu'à t = 0, uBC = E. On donne L = 20 mH et r suffisamment faible pour obtenir l'oscillogramme suivant : 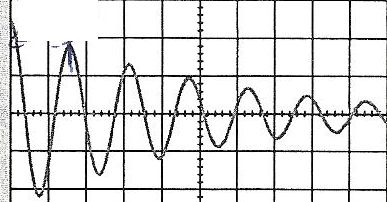Quel est le type de régime observé ? L'amplitude des oscillations iminue au cours du temps : régime pseudopériodique. Déterminer la pseudopériode si C = 1,25 mF. T = 2 p (LC)½ =2*3,14 (0,020 *1,25 10-3)½ =3,1 10-2 s = 31 ms. Donner une interprétation énergétique du phénomène observé. Lors des échanges d'énergie entre bobine et condensateur, une partie de celle-ci est dissipée par effet Joule dans les parties résistives du circuit. Quelles sont les sensibilités de l'oscilloscope ? Justifier. Choisir parmi les calibres des boutons ci-dessous : Tension initiale E = 12 V  ; 2,4 divisions sur l'axe vertical soit 5 V / div. Pseudopériode  : T = 31 ms représentée par 1,5 divisions soit  ~20 ms/div.

menu