|
|
On associe en
série un condensateur de capcité C, un conducteur ohmique de résistance
R = 104 ohms aux bornes d'un générateur idéal de tension de
fem E. A l'instant t=0, on ferme l'interrupteur K et on enregistre la
charge du condensateur à l'aide d'une interface reliée à un ordinateur.
Un dispositif aproprié permet de séparer sans danger la masse du
générateur est celle de l'interface. On souhaite voir apparaître :
- sur la voie 1, la tension u1 correspondant à l'évolution
de l'intensité i du courant ;
- sur la voie 2, la tension u2 correspondant à la tension
aux bornes du condensateur.
Sur
un schéma du montage faire apparaître les branchements de l'interface
et les tension u1 et u2.
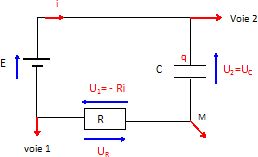
Préciser
en justifiant rigoureusement, sur chaque axe des ordonnées s'il s'agit
de la représentation de u1 ou -u1, u2 ou u2.
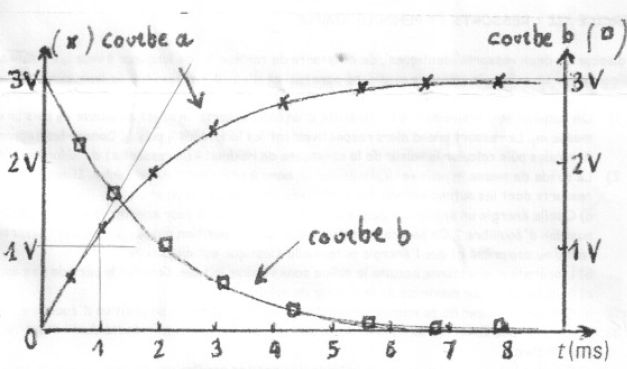
Courbe a :
u2, tension aux bornes du condensateur, fonction croissante
au cours de la charge jusqu'à la valeur uc=E.
Courbe b :
u1 = -UR=-Ri ; on a visualisé -u1 =
Ri, tension aux bornes du résistor, image de l'intensité au facteur R
près, fonction décroissante au cours de la charge jusqu'à la
valeur zéro.
Déterminer,
en détaillant la méthode, la constante de temps du circuit.
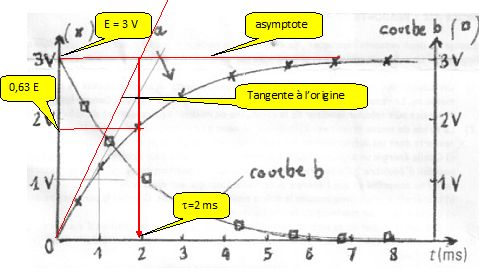
En
déduire la capacité C du condensateur.
C = t / R = 2 10-3
/ 104 = 2 10-7 F.
Déterminer,
en justifiant, à la fermeture de l'interrupteur :
La valeur de uc : la
continuité de l'énergie stockée par le condensateur conduit à uc(t=0)
= 0, le condensateur étant initialement déchargé.
La valeur de la charge q du condensateur : q(t=0) = 0, le condensateur étant
initialement déchargé.
La valeur de uR : additivité des tension uc(t=0)
+ uR(t=0 ) = E ; uR(t=0
) = E ;
La valeur de l'intensité du courant : i(t=0) =uR(t=0
) / R = E/R = 3/104 = 3 10-4 A.
Mêmes
questions en régime permanent.
uc= E =3 V; q = Cuc =CE = 2 10-7*3 = 6
10-7 C ; uR=0 ; i= 0.
|
| .
. |
.
Remontée d'un
ballon.
Un ballon sphèrique, de volume V = 4,2 10-3 m3,
de masse m = 25 g, est lâché sans vitesse initiale au fond d'une
piscine dont la profondeur est h = 2,50 m. On donne la masse volumique
de l'eau r = 1,0 103
kg m-3 et on prendra g = 9,81 m s-2.
Quelles
sont les forces qui agissent sur le ballon au cours de la montée ?
Donner leurs caractéristiques.
Le poids, verticale, vers le bas, valeur P = mg = 25 10-3*9,81
=0,24525 ~0,25 N.
La poussée d'Archimède, verticale, vers le haut, valeur r Vg = 1,0 103*4,2
10-3 *9,81 =41,2 ~41 N.
Une force de frottement fluide, verticale, vers le haut.
Ecrire
littérallement l'équation différentielle régissant le mouvement
en prenant une force de frottement fluide de la forme f = kv2
avec k = 6,975 S.I, v la vitesse du centre d'inertie du ballon et en
prenant un axe vertical Oz dirigé vers le haut.
Ecrire la seconde loi de Newton sur cet axe : - mg + r Vg -kv2 = mdv/dt.
dv/dt + k/m v2 = g(r V/m-1).
Montrer que l'on a dv/dt = 1638-279 v2 en unité S.I.
dv/dt + 6,975 / 0,025 v2 = 9,81(4,2 / 0,025-1) ; dv/dt +
279 v2 =1637.
A l'aide
de la méthode d'Euler, exprimer la vitesse vn en fonction de
vn-1, an-1, Dt.
( vn-vn-1 ) /Dt
= an-1 ; vn = vn-1+ an-1*Dt.
Faire de
même pour l'altitude zn en fonction de
zn-1, vn-1, Dt.
dz/dt = v ; (zn-zn-1) / Dt = vn-1 ; zn =
zn-1+ vn-1*Dt.
Calculer
les valeurs de z et de v pour un pas de 0,5 ms en se limitant à une
durée de 5 ms.
z0 = 0 ; v0 = 0, a0 =1638-279v02
= 1638 S.I.
v1 = v0 + a0Dt = 0 +1638*0,5 10-3
=0,819 ~0,82 m/s ; z1 = z0 + v0Dt = 0 ;
a1 = 1638-279 v12=1638-279*0,8192
=1451 SI ; v2 = v1 + a1Dt = 0,82 +1451*0,5 10-3
=1,55 ~1,5 m/s
; z2 = z1 + v1Dt = 0 +0,819*0,5 10-3 =4,1 10-4 m.
a2 = 1638-279 v22=1638-279*1,552
=967,7 SI ; v3 = v2 + a2Dt = 1,55 +967,7*0,5 10-3
=2,03 ~2,0 m/s
; z3 = z2 + v2Dt = 4,1 10-4 +1,55*0,5
10-3 =1,185 10-3 ~ 1,2 10-3 m.
a3 = 1638-279 v32=1638-279*2,032
=488,3 SI ; v4 = v3 + a3Dt = 2,03 +488,3*0,5 10-3
=2,27 ~2,3 m/s
; z4 = z3 + v3Dt = 1,185 10-3
+2,27*0,5 10-3 =2,32 10-3 ~ 2,3 10-3 m.
a4 = 1638-279 v42=1638-279*2,272
=200,3 SI ; v5 = v4 + a4Dt = 2,27 +200,3*0,5 10-3
=2,37 ~2,4 m/s
; z5 = z4 + v4Dt = 2,32 10-3
+2,37*0,5 10-3 =3,51 10-3 ~ 3,5 10-3 m.
a5 = 1638-279 v42=1638-279*2,372
=70,9 SI ; v6 = v5 + a5Dt = 2,37 +70,9*0,5 10-3
=2,405 ~2,4 m/s
; z6 = z5 + v5Dt = 3,51 10-3
+2,405*0,5 10-3 =4,71 10-3 ~ 4,7 10-3 m.
a6 = 1638-279 v62=1638-279*2,4052
=22,9 SI ; v7 = v6 + a6Dt = 2,405 +22,9*0,5 10-3
=2,416 ~2,4 m/s
; z7 = z6 + v6Dt = 4,71 10-3
+2,416*0,5 10-3 =5,92 10-3 ~ 5,9 10-3 m.
a7 = 1638-279 v72=1638-279*2,4162
=9,5 SI ; v8 = v7 + a7Dt = 2,416 +9,5*0,5 10-3
=2,42 ~2,4 m/s
; z8 = z7 + v7Dt = 5,92 10-3
+2,42*0,5 10-3 =7,13 10-3 ~ 7,1 10-3 m.
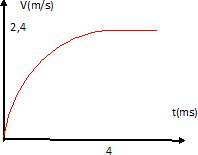
La vitesse limite obtenue par la méthode d'Euler est voisine de
2,42~2,4 m/s.
Par le calcul on obtient : 1638-279 vlim2 = 0 ; vlim
=(1638/279)½ =2,42 m/s.
A quelle
date peut-on considérer que le ballon a atteint cette limite ? Quelle
est alors la distance parcourue par le ballon depuis l'instant du
lâcher ? Que peut-on conclure sur le mouvement du ballon ?
A partir de 4 ms, on peut considérer que cette vitesse limite est
atteinte. Le ballon a parcouru environ 6 mm. Le mouvement du ballon est
ensuite rectiligne uniforme, d'après le principe d'inertie.
Déterminer
au bout de combien de temps le ballon a atteint la surface.
h / vlim ~2,5 / 2,4 ~1 s.
Ressorts et
pendule simple.
On dispose de deux ressorts identiques, de constante de raideur k, de
longueur à vide L0
et de masse négligeable, d'un solide de masse m considéré comme
ponctuel et d'un fil inextensible de longueur L, lui aussi de masse
négligeable.
On suspend à l'extrémité d'un ressort un objet de masse m1
puis un autre de masse m2. Le ressort prend les longueurs
respectives L1 puis L2.
Donner les expressions littérales puis
calculer k et L0.
m1 = 100 g ; m2 = 200 g ; L1 = 32,9 cm
; L2 = 45,8 cm ; m=254 g ; g = 9,8 N / kg.
A l'équilibre m1g = k(L1-L0) et m2g = k(L2-L0)
; m1/ m2 = (L1-L0) /(L2-L0) ;
m1(L2-L0) =m2(L1-L0)
; L0( m2-m1) =m2L1-m1L2 ; L0
= (m2L1-m1L2 ) / ( m2-m1).
L0 (0,2*0,329-0,1*0,458)
/ 0,1 =0,200 m = 20,0 cm.
k = m1g / (L1-L0) =0,1*9,8 / 0,129 =7,60 N/m.
Le solide de masse m
peut se déplacer sur un banc à coussin d'air horizontal. Il est
solidaire des ressorts dont les autres extrémités sont fixées en des
points M et N.
Quelle énergie un opérateur doit-il apporter aux ressorts pour écarter la masse de 5,0 cm de sa position d'équilibre
? On pourra considérer que dans la position initiale, aucun des
ressorts n'est tendu ou comprimé et que l'énergie potentielle élastique
est alors nulle.
Le système est équivalent à un ressort unique de constante de raideur 2k.
L'énergie mise en oeuvre est égale à : ½(2k)(L-L0)2 =0,5*2*7,60 *0,052 =1,9 10-2 J.
L'opérateur abandonne ensuite le solide sans vitesse initiale. Calculer la période des oscillations.
T = 2p(m/(2k))½ =6,28(0,254/(2*7,60))½ =0,812 ~0,81 s.
Calculer la vitesse maximale du solide.
La vitesse est maximale au passage à la position d'équilibre. La conservation de l'énergie mécanique conduit à :
½mvmax2 = 0,019 ; vmax =(2*0,019/0,254)½ =0,387 ~0,39 m/s.
Calculer sa vitesse lorsqu'il se trouve à 3,0 cm de sa position d'équilibre.
Energie potentielle élastique : ½(2k)(L-L0)2 =0,5*2*7,60 *0,032 =6,84 10-3 J.
La conservation de l'énergie mécanique permet le calcul de l'énergie cinétique : 1,9 10-2 - 6,84 10-3 =1,216 10-2 J.
½mv2 = 0,0216 ; v =(2*0,0216 / 0,254)½ =0,3094 ~0,31 m/s.
On accroche le solide à l'extrémité du fil de longueur L ; l'autre extrémité du fil est fixée à un support fixe.
Calculer L pour que les petites oscillations du pendule ainsi constitué soit la même que celle du pendule élastique précédent.
T = 2p (L/g)½ ; L = T2g / (4p2) =0,812 *9,8 / (4*3,142) =0,163 m ~16 cm.
L'opérateur apporte la même énergie au pendule simple que celle apportée au pendule élastique.
Calculer l'amplitude angulaire q du mouvement.
Energie potentielle maximale du pendule ( origine à la position d'équilibre) : m g L( 1-cos q).
Conservation de l'énergie mécanique : 0,019 = m g L( 1-cos q).
1-cos q) = 0,019/(mgL) ; cos q =1-0,019/(mgL) = 1-0,019 / (0,254*9,8*0,163) =0,953 ; q = 17,6 ~18°.
|
|

