Comment alimenter un moteur à l'aide d'une bobine : concours audioprothésiste Paris 2004.

. .

Propriétés d'une bobine. Un circuit électrique comprend en série : un générateur de tension constante de force électromotrice E = 9,0 V, un interrupteur K, une bobine d'inductance L et de résistance r, un conducteur ohmique de résistance R. Un ordinateur muni d'un système d'acquisition et d'un logiciel de traitement des données permet de visualiser les variations de la tension UR aux bornes du conducteur ohmique. Faire le schéma du circuit et y figurer les branchements des deux bornes EAO ( borne positive ) et M( bornne négative)  de l'interface reliée à l'ordinateur qui permettent de visualiser la tension UR. On ferme l'interrupteur à la date t=0.  Donner l'allure de la courbe UR = f(t) sans souci d'échelle. Interpréter qualitativement cette courbe. La tension UR et l'intensité sont proportionnelles. On  observe un retard à l'établissement du courant. Pendant le régime transitoire, la bobine stocke de l'énergie. Etablir l'équation différentielle vérifiée par la tension uR. Additivité des tensions uR + uL = E avec uL = Ldi/dt + ri et i = uR/R ; di/dt = 1/R duR/dt. uR + L/RduR/dt + r/R uR = E. (R + r)/ L uR + duR/dt  = R/L E. (1). Montrer que cette équation différentielle a une solution de la forme uR(t) = U(1-exp(-t / t )) avec U = RE/(r+R) et t = L/(r+R). duR/dt = U/ t exp(-t / t ), repport dans (1) : (R + r)/ LU(1-exp(-t / t )) + U/ t exp(-t / t ) = R/L E. (R + r)/ LU +(U/ t -R + r)/ LU )exp(-t / t ) = R/L E. Cette égalité est vérifiée quel que soit le temps si : (R + r)/ LU =  R/L E soit U = RE/(r+R) et  si U/ t =(R + r)/ LU soit t = L/(r+R). Montrer que t est homogène à un temps. Energie stockée par la bobine : ½LI2 ; L 'exprime en J A-2. Energie dissipée par effet Joule RI2t soit R exprimée en J A-2 s-1. Par suite t =L/(R+r) s'exprime en seconde. . . .  . Application : On introduit dans la bobine précédente un noyau de fer doux et on la place dans un circuit comportant un moteur M. 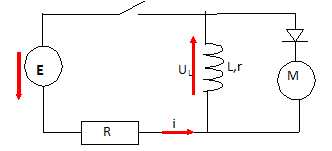Pourquoi a-t-on introduit un noyau de fer doux dans la bobine ? L'inductance, et en conséquence l'énergie stockée par la bobine, augmentent. Après fermeture de l'interrupteur, au bout de combien de temps peut-on considérer que le régime permanent est atteint ? On donne L = 1 H, r = 10 ohms et R = 80 ohms. t = L/r+R) = 1 / 90 = 0,011 s. Le régime permanent est atteint au bout de 5t soit environ 0,056 s. Le moteur tourne-t-il lorsque le régime permanent est atteint ? Justifier. Le moteur est en série avec une diode non passante : le moteur ne tourne pas. Calculer l'énergie stockée dans la bobine lorsque le régime permanent est atteint. Sous quelle forme est-elle stockée ? L'énergie est stockée sous forme électromagnétique. ½LI2 avec I = E/(R+r) = 9,0 / 90 = 0,10 A. ½LI2 = 0,5 * 1 *0,01 = 0,005 J. On ouvre l'interrupteur et le moteur tourne quelques instants. Indiquer le sens du courant dans le circuit pendant que le moteur tourne. La continuité de l'énergie stockée par la bobine conduit à la continuité de l'intensité : la diode devient passante. Un petit objet de masse m = 5 ,0 g a été suspendu à l'arbre du moteur par l'intermédiaire d'un fil. Sur quelle hauteur h cet objet a été soulevé depuis l'ouverture de l'interrupteur jusqu'à l'arrêt du moteur ? ( g ~ 10 SI ). L'énergie électromagnétique est conveertie en énergie mécanique ( énergie potentielle de pesanteur ) : 0,005 = m g h h = 0,005 / (mg) =0,005 / (0,005*10) = 0,10 m.

menu