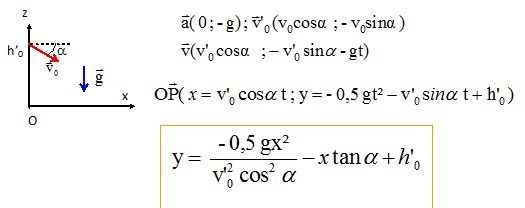|
.
|
|
Résonance d'intensité.
On
veut mesurer la valeur L de l'inductance d'une bobine. Pour cela on
alimente par un générateur de tension sinusoïdale un circuit composé
d'un conducteur ohmique de résistance R = 100 ohms, d'un condensateur
de capacité C = 470 µF et la bobine d'inductance L et de résistance r =
25 ohms.
Pour la fréquence f0 = 500 Hz on a la résonance du circuit.
Quelle
est la signification physique de la résonance ?
L'impédance
du dipole RLC est minimale : l'intensité du courant passe par une
valeur maximale et on observe une surtension aux bornes du condensateur.
Calculer
la valeur de L.
A la résonance LC ( 2 p f0)2
= 1.
L = 1 / (C ( 2 p f0)2)
= 1 / (470 10-6* ( 1000 p )2) = 2,156 10-4
~2,16 10-4 H.
La tension efficace délivrée par le générateur vaut U = 10 V.
En déduire
l'intensité efficace I du courant dans le circuit au moment de la
résonance.
L'impédance est égale à la résistance totale du
circuit : R+r = 125 ohms.
I = U / (R+r) = 10 / 125 = 0,080 A.
La bobine ne peut pas supporter une intensité supérieure à 300 mA ; aurait-on pu faire
la même expérience sans mettre de conducteur ohmique dans le circuit
?
L'impédance est
égale à la résistance totale du circuit : r = 25 ohms.
I = U / r = 10 / 25 = 0,40 A = 400 mA.
Cette
valeur est supérieure à 300 mA, il ne faut pas faire l'expérience sans
conducteur ohmique R.
|
| .
. |
Lancer d'une balle de tennis.
g = 9,81 m s-2 ; la balle de tennis de masse m sera assimilée à son centre d'inertie et les forces de frottement sont négligées.
Le joueur lance la balle verticalement vers le haut à partir d'une hauteur h0 = 2,00 m et avec une vitesse initiale v0 = 4,50 m/s.
Quelle est l'altitude maximale atteinte ?
Energie mécanique initiale : mgh0 +½mv02.
Energie mécanique au point le plus haut ( vitesse nulle) : mg hmax.
Conservation de l'énergie mécanique : mgh0 +½mv02 = mg hmax.
hmax = h0 +½v02 / g = 2,00 +0,5 *4,52 / 9,81 = 3,03 m.
Au cours du match, le joueur frappe la balle lorsque celle-ci est en I à une hauteur h'0 = 2,30 m du sol et lui communique une vitesse v'0 = 108 km/h dirigée vers le sol et faisant un angle a = 20 ° avec l'horizontale.
Etablir que l'équation de la trajectoire est :
z = -½g x2 / (v'02 cos2a) -x tan a + h'0.
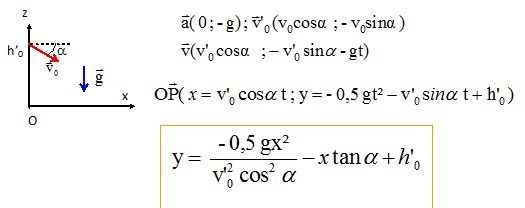
Le filet de hauteur 0,92 m est situé à 3,00 m du joueur.
Sa balle passera-t-elle au dessus du filet ?
v'0 = 108 / 3,6 =30 m /s.
y(3,0) = -0,5 *9,81*9 /(30 cos 20)2 -3 tan 20 +2,30 = -0,0555 -1,092 + 2,30 =1,15 m.
La balle passe donc au dessus du filet..
|
Oscillateur élastique horizontal.
Un
solide de masse m = 200 g pouvant glisser sans frottement sur un plan
horizontal est relié à un ressort. L'autre extrémité du ressort est
reliée à un point fixe A. Constante de raideur k = 5,00 N /m.
On pousse le solide vers la gauche de a = 3,00 cm et on le lâche sans vitesse initiale.
Faire le bilan des forces appliquées au solide dans le cas où le ressort est comprimé. Faire le schéma correspondant.
Le solide S est soumis à son poids, à l'action du plan et à une force de rappel exercée par le ressort.
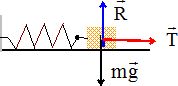
Donner l'expression de la période T et la calculer.
T = 2 p (m/k)½ = 2 *3,14 (0,200 / 5,00)½ =1,257 ~1,26 s.
Calculer les énergies cinétique et potenteille élastique du système au moment du lâcher.
Le lâcher se fait sans vitesse, l'énergie cinétique initiale est nulle.
Energie potentielle élastique : ½k a2 = 0,5*5*0,092 =2,25 10-3 J.
En déduire la valeur de la vitesse au passage à la position d'équilibre.
Energie mécanique initiale : 2,25 10-3 J.
Au passage à la position d'équilibre, l'énergie mécanique est sous forme cinétique : ½mv2.
Conservation de l'énergie mécanique : ½mv2 = 2,25 10-3.
v = (2* 2,25 10-3 / 0,200)½ =0,15 m/s.
|
|