Charge d'un condensateur à courant constant :  concours kiné Assas 2012.

. .

ll est demandé les expressions tittérales simptifiées et ordonnées avant toute apptication numérique. les notations du texte doivent êre scrupuleusement respectées. Un condensateur est dit idéal si I'isolant entre ses armatures est parfait, et donc si aucun électron parvient à passer d'une armature à I'autre. On relie en série un condensateur idéal de capacité C, initialement déchargé, un résistor de résistance r, un interrupteur K initialement ouvert, et un générateur de courant délivrant une intensité constante I0. 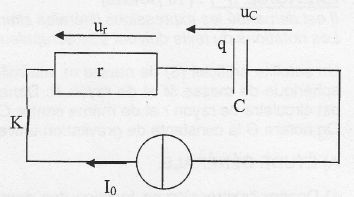À t = 0, on ferme l'interrupteur K, selon te schéma ci-dessous. À quelle équation différentielle simple obéit la charge q(t) ? dq(t) / dt = I0. Donner sans démonstration les expressions, en fonction du temps et des données de l'exercice, de q(t), uc et ur. Représenter les graphes de uc(t) et ur(t). ( Noter clairement sur les graphes les expressions des ordonnées à l'origine et des pentes ). q(t)= I0t.( droite de pente I0 passant par l'origine ). uc(t) = q(t) / C = I0 / C t.( droite de pente I0 / C passant par l'origine ). ur(t) = r I0.  ( droite horizontale d'ordonnée à l'origine r I0 ). . . . 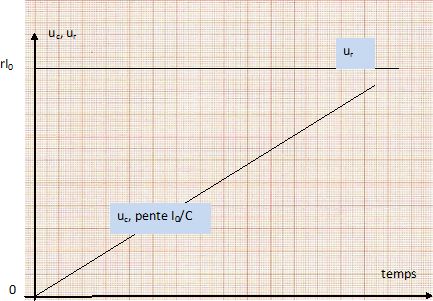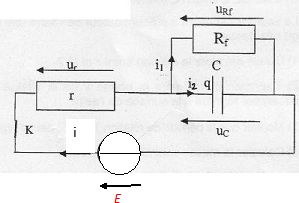Charge d'un condensateur réel à courant constant. En réalité, un condensateur, même isolé, se décharge lentement. Ceci est dû aux électrons qui parviennent à passer d'une armature à l'autre, I'isolant séparant ces armatures ne pouvant pas être parfait, Ce phénomène peut être modélisé par un rsistor, appelé << résistance de fuite », notée Rf, placé en parallèle d'un condensateur idéal. Le montage précédent devient donc celui reproduit ci-dessous. 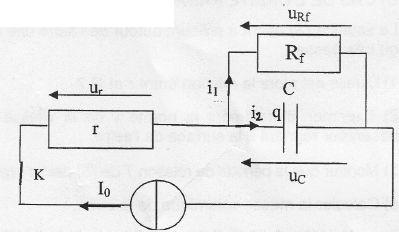Le condensateur est initialement àéchargé. À t = 0, on ferme I'interrupteur K.  Etablir la relation entre i1 et q(t). i1 = uRf / Rf ; uRf  = uc =q(t) / C ;  i1 = q(t) / (Rf C). En appliquant la loi des noeuds, établir l'équation différentielle à laquelle obéit q(t). I0 = i1 +i2 ; i2 = dq(t)/dt ; I0 = q(t) / (Rf C) +  dq(t)/dt. (1) La solution de l'équation différentielle précédente est de la forme : q(t) = A(1- exp(-t/t)). Déterminer les expressions des constantes A et t en fonction des données de l'exercice. Que représentent ces constantes ? dq(t)/dt = A / t exp(-t/t) ; repport dans (1) : I0 = A(1- exp(-t/t)) / (Rf C) +  A / t exp(-t/t) = A +A( 1 / t - 1/ (Rf C))exp(-t/t). Par suite : A / (Rf C)= I0 ; A = I0 Rf C, charge finale du condensateur. et t = Rf C, constante de temps du dipole RC. Donner les expressions, en fonction des données de l'exercice, de uc(t) et de i2. Tracer les graphes de ces fonctions. (Noter clairement sur ces graphes les grandeurs remarquables : ordonnées à l'origine, asymptotes...etc...). uc(t) =q(t) / C = I0 Rf (1- exp(-t/t)) ; i2(t) = dq(t)/dt = I0  exp(-t/t). 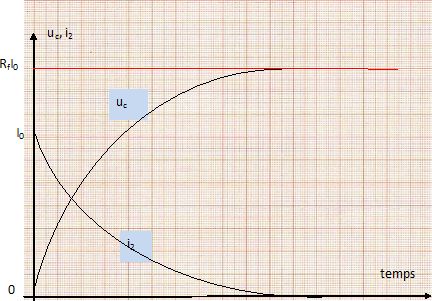Charge d'un condensateur réel à tension constante. On reprend le montage précédent, mais on remplace le générateur de courant par un générateur idéal de tension constante E soit i(t) le courant délivré par cerui-ci.- Reproduire.sur votre copie le schéma de ce nouveau circuit. Le condensateur est initialement déchargé. À t = 0, on ferme I'interrupteur K.  En se servant de la relation entre i1 et q(t) et en utilisant la loi des noeuds, trouver l'expression du courant i(t) en fonction de q(t) et de sa dérivée. i1 = q(t) / (Rf C) ; i(t)= i1 +i2 ; i2 = dq(t)/dt ; i(t) = q(t) / (Rf C) +  dq(t)/dt. Etablir l'équation ditférentielle à laquelle obéit q(t). Additivité des tensions : E = uc +ur = Cq(t) +r i = q(t)/ C + r q(t) / (Rf C) + r dq(t)/dt. dq(t)/dt + (1 / (rC) +1/(Rf C) )q(t) = E/r. Montrer qu'elle s'écrit sous la forme dq(t)/dt + (1 / (arC)q(t) = E/r. Donner l'expression de a. (1 / (rC) +1/(Rf C) = (r + Rf) / (rRf C) ; on pose a = Rf / (r + Rf).  dq(t)/dt + (1 / (arC)q(t) = E/r. La solution de l'équation différentielle précédente est de la forme : q(t) = A(1- exp(-t/t)). Donnez sans démonstration les expressions des constantes A et t en fonction des données de l'exercice. A : charge finale constante de la charge (1 / (arC)A = E/r. A = E a  C et t = arC. Quelle est l'influence de la résistance de fuite sur la charge du condensateur ? Justifier succincternent. La charge maximale du condensateur est inférieure à EC, le coefficient a étant inférieur à 1. Si Rf augmente, la charge maximale tend vers EC.

menu