|
.
|
|
Champ magnétique.
Plaçons
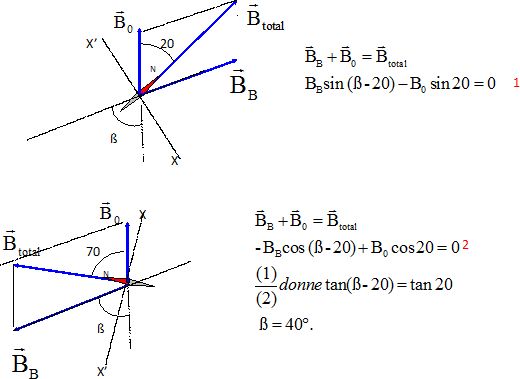
une boussole horizontale au centre d'un solénoïde d'axe horizontal.
Quand un courant électrique circule dans le solénoïde, l'aiguille de la
boussole dévie de 20° vers l'est. En inversant le sens du courant,
l'aiguille dévie de 70 ° vers l'ouest.
Quel
est la valeur de l'angle entre l'axe du solénoïde et la direction
nord-sud ?
Projection sur un axe perpendiculaire au
champ total, différent dans les deux cas.
On
démontre que la valeur du champ magnétique au centre de la bobine de
longueur L et de diamètre D comportant N spires et parcourue par un
courant I est : B = µ0NI / (L2 + D2)½.
Que
devient cette expression si L est très supérieur à D ? Quel dispositif
connu retrouve-t-on ?
B = µ0NI /L ; c'est le cas d'un
solénoïde.
Que
devient cette expression si D est très supérieur à L ? Exprimer le
champ au centre de la bobine plate en fonction de son rayon R, N et I.
B = µ0NI /D = µ0NI
/(2R).
On emboîte deux solénoïdes ayant respectivement n1 et n2
spires par mètre, en faisant coîncider leurs axes. On branche ces deux
bobines en série et en faisant circuler un courant d'intensité I, on
peut obtenir au centre du montage un champ magnétique de valeur B ou un
champ magnétique de valeur 2B.
Que
vaut le rapport n2/n1 ?
Les deux champs magnétiques de même direction ont le même sens : µ0n1I
+µ0n2I = 2 B.
Les champs magnétiques de même direction sont de sens contraire :
µ0n1I
-µ0n2I = B.
n1
+ n2 = 2B/ (µ0I) n1 - n2 = B/ (µ0I) ; n1 + n2 = 2(n1
- n2).
1+ n2 / n1
= 2-2n2 / n1 ; 3n2 / n1 = 1 ; n2
/ n1 = 1/3.
|
.
Champ de
pesanteur.
On considère une piste ABC constituée d'une partie rectiligne AB
horizontale de longueur d, suivie d'une partie BC sous forme d'un arc
de parabole d'équation y = ax2, l'extrémité C est telle que xC
= +d.
On lance un bloc de masse m, que l'on assimilera à un point matériel, à
partir du point A avec un vecteur vitesse horizontal orienté suivant le
sens positif.
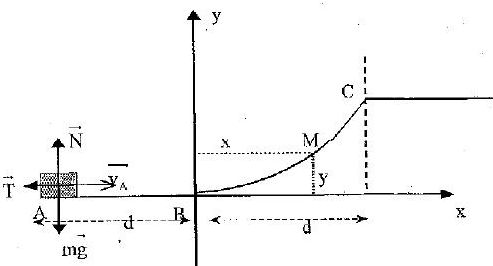
T : force de frottement solide ; N : réaction normale
de la piste. Lorsque le bloc glisse sur la piste T = f N où f est le
coefficient de frottement solide caractérisant la liaison bloc-piste.
On donne m = 100 g ; f = 0,1 ; a = 0,05 m-1 et g = 10 m s-2.
Exprimer
T en fonction de f, m et g.
Sur la partie horizontale AB : N = mg ; T = f N = f m g.
Quelle
est l'expression de la vitesse minimale vmin à donner au bloc
pour qu'il s'arrête tout juste en B ?
Th de l'énergie cinétique entre A et B ; seul T travaille WT
= -T d = -f m g d.
0-½m v2min = -f m
g d ; vmin = (2f g d)½.
On lance le bloc à partir de A avec une vitesse initiale v0
> vmin et on néglige les frottement sur la partie BC de
la piste.
Exprimer vM, la vitesse du bloc
au point M.
Th de l'énergie cinétique entre A et
M ; WT = -T d = -f m g d.
Travail du poids entre B et M : -m g y; L'action normale du plan,
perpendiculaire à la vitesse, ne travaille pas.
½m v2M -½m v20 = -f m g d -mg y ; v2M
= v20 -2g(f d+y) ; vM = (v20
-2g(f d + y))½.
Pour
quelle valeur de d0 de d le bloc
arrivera-t-il en C avec une vitesse nulle ? On donne v20= 3 SI.
v2C =0 = v20 -g(f
d0+ad02) ; -3 + 2d0 +d02=0.
D =4+4*3 =16 ; D½ = 4 ; d0
=(-2 +4) / 2 = 1,0 m.
| Champ gravitationnel.
Un
satellite artificiel de masse m est placé sur une orbite circulaire
dans le plan de l'équateur, à une altitude h au dessus de la surface de
la terre de masse M et de rayon R.
Déterminer
l'unité SI de la constante de gravitation.
Force de gravitation exercée par la terre sur le satellite. F = GMm /
(R+h)2. G = F (R+h)2
/ (Mm).
[F] = kg m s-2 ; [G] =kg m s-2
m2 kg-2 = kg-1
m3 s-2.
Déterminer
l'expression du vecteur accélération et de la valeur de la vitesse v du
satellite.
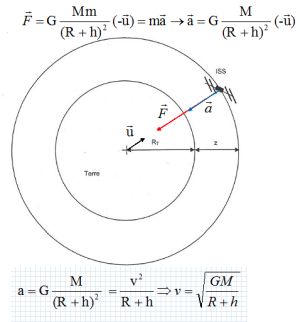
La période de révolution de la terre autour d'elle même est T0
= 24 heures.
Déterminer
l'expression de l'altitude h d'une orbite circulaire occupée par un
satellite qui paraît immobile à la verticale d'un observateur
terrestre.
Le satellite géostationnaire d'écrit la circonférence 2p(R+h) à la vitesse v pendant la
durée T0.
2p(R+h) = vT0 =(GM)½
T0 / (R+h)½.
(R+h)1,5 = (GM)½ T0 /(2p) ; (R+h)1,5
= [(GM) T02 /(4p2)]1/3 ;
h = [(GM) T02
/(4p2)]1/3 -R.
On désigne par g(h) la valeur du champ de gravitation à l'altitude h et
g0 = 10 m s-2 sa valeur à la surface de la terre.
Déterminer
l'expression de g(h).
g0 = GM/R2 ; g(h) = GM/(R+h)2 ; g(h) =
g0R2/(R+h)2.
Un vaisseau spatial erre dans le cosmos, très loin de tout astre
ou de toute planète. Le vaiseau n'a pas de hublots et les éventuels
moteurs sont très silencieux.
Quelle
impression les passagers ressentent-ils ?
Les passagers ont l'impression d'être immobiles et en impesanteur.
Le pilote met en marche les réacteurs qui communiquent au vaiseau une
acélération constante a = 2 g.
Quel
changement les passagers éprouvent-ils et que peuvent-ils conclure
?
Les passagers subissent l'accélération a = 2g et sont plaqués contre
leurs sièges. Ils ressentent une impression de pesanteur et pensent que
l'accélération est équivalente à la pesanteur.
Le vaiseau spatial se place au point E d'équigravité terre-lune. La
distance des centre des astres est notée d et MT = 81 ML.
Déterminer
l'expression de la position de ce point en prenant le centre de la
terre comme origine.
En E, on considère un objet de masse m = 1 kg et on
note x la distance du centre de la terre au point E.
Force exercée par la terre sur l'objet : F =GMT/x2
;
Force exercée par la lune sur l'objet : F =GML/(d-x)2
;
GMT/x2 = GML/(d-x)2
; (MT/ML)½ = 9 = x / (d-x).
9 d - 9x = x ; x = 0,9 d.
|
|


