|
|
Une pompe hydraulique débite 300 m3 h-1 d'eau froide. Sa conduite d'aspiration a un diamètre d1 =200 mm. Sa conduite de refoulement a un diamètre d2 = 100 mm.
On négligera les pertes de charge dans cette étude.
Masse volumique de l'eau r = 1000 kg m-3 ; g = 9,8 m s-2 ; pression atmosphérique p0 = 1,00 105 Pa.
Equation de Bernoulli : (p2-p1) +r g ( z2-z1) +½r(v22-v21) = P / Qv.
P : puissance de la machine et Qv débit volumique ( m3 s-1).
Calculer la vitesse d'écoulement v1 dans la conduite d'aspiration.
S : section de la conduite ; S = 3,14 *d21/4 =3,14 *0,202/4 =3,1416 10-2 m2.
Qv = 300 / 3600 = 8,33 10-2 m3 s-1.
v1 = Qv / S = 8,33 10-2/ 3,1416 10-2 =2,6526 ~2,65 m s-1.
Calculer la vitesse d'écoulement v2 dans la conduite de refoulement.
Le
débit volumique reste constant ; le diamètre de la conduite de
refoulement est égal à la moitié du diamètre de la conduite
d'aspiration.
v2 = 4 v1 = 10,610 ~10,6 m s-1.
|
.
.
|
.
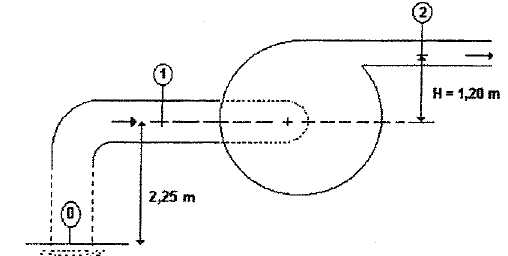
La pompe aspire l'eau stagnante d'un bassin ouvert situé à 2,25 m au dessous du niveau (1), d'entrée de la pompe.
Calculer la pression p1 à l'entrée de la pompe en (1).
Appliquer le théorème de Bernoulli entre la surface de l'eau stagnante ( point 0 ) et le point (1) :
(p1-p0) +r g ( z1-z0) +½r(v21-v20) = 0 avec v0 = 0 ; z1-z0 = 2,25 m.
p1=p0 +r g ( z1-z0) +½r(v21-v20)
p1=1,00 105 -1000*9,8*2,25 -500*2,652 =1,00 105 -2,205 104 -3,51 103 =7,4439 104 ~7,44 104 Pa.
Calculer le débit massique Qm en kg s-1.
Qm = Qv r = 8,33 10-2 *1000 = 83,3 kg s-1.
On donne la pression à la sortie de la pompe p2 = 1,60 105 Pa.
Calculer la puissance mécanique de la pompe pour ce débit.
Appliquer le théorème de Bernoulli entre le point (2) et le point (1) :
P = Qv [ (p2-p1) +r g ( z2-z1) +½r(v22-v21) ].
P = 8,33 10-2 [1,60 105- 7,44 104+9800*1,2 +500(10,62-2,652) ].
P = 8,33 10-2 [ 8,556 104+1,176 104 +5,27 104 ] = 1,25 104 W = 12,5 kW.
Cette pompe est actionnée par un moteur électrique. Le rendement global du groupe est 80 %.
Calculer la puissance électrique consommée.
12,5/0,8 =15,6 kW.
|
|
