Capteur de niveau : concours technicien supérieur de l'industrie et des mines 2012.

. .

Le contrôle de niveau dans une cuve peut être réalisé à l'aide d'une sonde capacitive. On se propose d'étudier le principe d'une telle sonde puis la génération d'un signal électrique qui pourra servir à déclencher une électrovanne. La sonde capacitive est assimilable à un condensateur cylindrique. Une tige métallique cylindrique plongée au centre de la cuve forme la première armature du condensateur. cette tige est recouverte d'une mince couche d'isolant ( téflon ). La cuve, également métallique et cylindrique, joue le rôle de deuxième armature. Le condensateur ainsi formé possède une capacité C qui dépend du niveau de liquide dans la cuve. 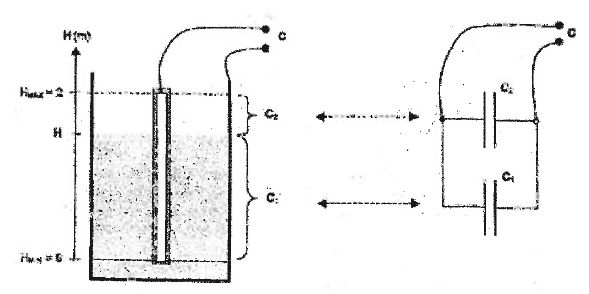Le niveau H de liquide permet de décomposer, en première approximation, le condensateur cylindrique en deux condensateurs comme le montre la figure : - un condensateur de capacité C1 de diamètre intérieur d1 = 10 mm et de diamètre extérieur d2 = 12 mm dont le diélectrique est seulement le téflon, le liquide étant conducteur et en contact avec la cuve. - un condensateur de capacité C2 de diamètre intérieur d1 = 10 mm et de diamètre extérieur d'2= 2,6 m dont le diélectrique est principalement l'air, l'épaisseur du téflon étant négligeable. La capacité C d'un condensateur cylindrique a pour expression : . . . Exprimer C1 en fonction de la hauteur de liquide H. Pour le téflon er = 2,1. C1 = 2 p e0 er H / ln(d2 / d1).  Exprimer C2 en fonction des hauteurs H et Hmax. Pour l'air er = 1,0. C2 = 2 p e0 (Hmax-H) / ln(d'2 / d1). Donner l'expression de la capacité équivalente C à l'association en parallèle des deux condensateurs en fonction de C1 et C2. C = C1+C2. Montrer que C peut se mettre sous la forme C = aH + b où l'on exprimera a et b en fonction des données. C = 2 p e0 er H / ln(d2 / d1) + 2 p e0 (Hmax-H) / ln(d'2 / d1). C = 2 p e0 (er / ln(d2 / d1) -1/ ln(d'2 / d1) ) H + 2 p e0 Hmax / ln(d'2 / d1).  a = 2 p e0 (er / ln(d2 / d1) -1/ ln(d'2 / d1) ) ; b = 2 p e0 Hmax / ln(d'2 / d1). On donne Hmax = 2 m. Montrer que C = 630 H + 20 avec C en pF.  a = 2*3,14 *8,85  (2,1 / ln(12 / 10) -1/ ln(2,6 / 0,01) ) = 630 pF m-1. b = 2*3,14 *8,85 *2 / ln(2,6 / 0,01) = 20 pF. En déduire la plage de variation de C correspondant à une différence de niveau allant de zéro à 2 m. Cmin = 20 pF ; Cmax = 630*2 +20 =  1,28 103 pF. 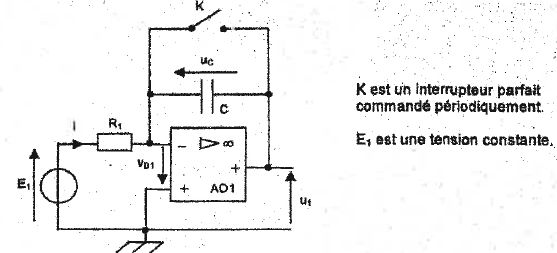Le condensateur précédent est intégré dans le circuit suivant : L'AO est supposé idéal et fonctionne en régime linéaire. Que peut-on en déduire pour la tension VD1 ? VD1 = 0. Etablir une relation entre les tensions u1 et uC. u1 + uC +VD1 = 0 ;  u1 = - uC. L'interrupteur est fermé. Que vaut uC ? Aux bornes d'un interrupteur fermé, la tension est nulle. A t = 0, K s'ouvre. On considère que u1(0) = 0 V. Exprimer i en fonction de E1 et R1. E1 +(- R1i )+ VD1 ;  i = E1 / R1. Exprimer i en fonction de C et duC/dt puis en fonction de C et du1/dt. q = CuC ; i = dq/dt ; i = C duC/dt  = -Cdu1/dt. Exprimer du1/dt en fonction de E1, R1 et C. E1 / R1 = -Cdu1/dt ; du1/dt = -E1 / ( CR1 ). 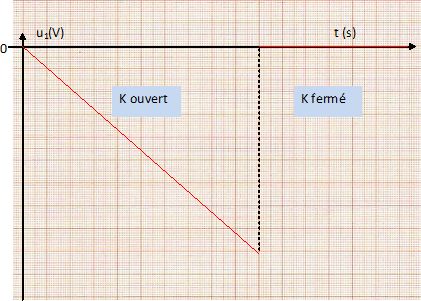En déduire l'expression de u1 en fonction du temps. Représenter l'allure de u1 en précisant pour les différentes portions de la courbe l'état de l'interrupteur " ouvert" ou " fermé". K ouvert : u1 = -E1 t / ( CR1 ) + constante. A t = 0, u1(0)=0 d'où : u1 = -E1 t / ( CR1 ).  K fermé : u1 =0.

menu