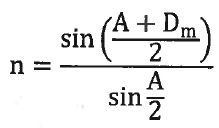|
|
La
détection et la détermination de la concentration de certains polluants
peut être réalisée par spectrophotométrie visible ou UV. Le domaine
visible est environ limité par les longueurs d'ondes dans le vide l1 = 400 nm et l2 = 800 nm.
Nommer et situer les domaines de radiations situés au-delà de chacune de ces limites.
Ultraviolet ( UV) : longueurs d'onde dans le vide inférieures à 400 nm.
Infrarouges ( IR), longueurs d'onde dans le vide supérieures à 800 nm.
Calculer les fréquences v1 et v2 des radiations limites du visible.
n1 = c / l1 = 3,00 108 / (400 10-9) = 7,50 1014 Hz.
n2 = c / l2 = 3,00 108 / (800 10-9) = 3,75 1014 Hz.
En
spectroscopie visible, le dispositif permettant de sélectionner la
longueur d'onde est constitué d'un système dispersif comme un prisme.
Un prisme constitué par un matériau transparent, homogène, isotrope,
d'indice supérieur à 1, se trouve plongé dans l'air dont l'indice sera
pris égal à 1.
Formules du prisme : Les orientations des angles sont choisies pour que les valeurs des angles i, i', r, r' et D soient positives.
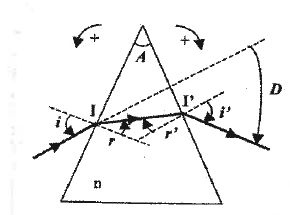
Exprimer
les lois de Snell-Descartes en fonction de i, i', r, r' et n,
traduisant les réfractions à l'entrée I et à la sortie I' du prisme.
En I : sin i = n sin r ; en I' : n sin r' = sin i'.
Déterminer
les relations géométriques liant les angles A, r et r' d'une part et
l'angle de déviation D aux angles A, i et i' d'autre part.
La somme des angles dans le triangle AII' vaut 180 ° :
A + (90-r) +(90-r') = 180 ° ; A = r + r'.
D = i-r + i'-r' = i + i' - A.
|
| .
. |
.
Minimum de déviation.
Expérimentalement, en lumière monochromatique, on met en évidence l'existence d'un minimum de déviation, noté Dm,
quand l'angle d'incidence varie. Le tracé du rayon lumineux est alors
symétrique par rapport au plan bissecteur de l'angle A du prisme.
Faire le schéma correspondant à cette situation.
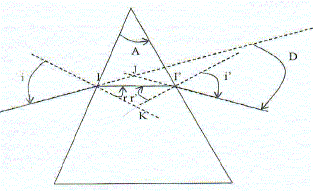
Préciser alors les relations entre les angles i et i' d'une part, puis r et r' d'autre part.
Du fait de la symétrie : i = i'.
sin i = n sin r ; n sin r' = sin i' d'où : n sin r = n sin r' ; r = r'.
Montrer que la relation donnant l'indice n en fonction de l'angle A et de la déviation minimale Dm s'écrit : 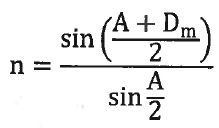
rmini = r'mini = ½A ;
or D= i+i'-A soit Dmin
= 2imin -A ;
imin =½ ( Dmin +A
)
de plus sin imin = n
sin(½A) d'où : n = sin[½ (
Dmin +Amin )] / sin(½A).
Sélection de la longueur d'onde de travail.
Après
avoir rappeler la définition de l'indice de réfraction d'un milieu,
expliquer qualitativement que la déviation minimale dépend de la
longueur d'onde de travail.
L'indice de réfraction d'un milieu transparent, noté n ( n supérieur à 1) est
égal au rapport de la célérité de la lumière dans le vide ( 3 108
m/s) à la célérité de la lumière dans le milieu transparent.
Un prisme est dispersif : la célérité de l'onde en propagation dans ce
milieu dépend de sa féquence. L'indice de réfraction dépend de la célérité donc de la fréquence de
l'onde.
Dm varie avec la longueur d'onde de la lumière incidente ;
en effet l'indice d'un matériau varie avec l selon la Loi de Cauchy : n = P +
Q/l2.
|
|