.
|
|
Quelle est la position des planètes dans le système solaire, par ordre croissant de la distance les séparant du soleil ?
A) Vénus ; Mercure ; Mars ; Terre ; Jupiter ; Saturne.
B ) Vénus ; mercure ; Terre ; Mars ; Saturne ; Jupiter.
C ) Mercure ; Vénus ; Terre ; mars; Jupiter ; Saturne. Vrai.
D ) Mercure ; vénus ; Mars ; Terre ; Saturne ; Jupiter.
E) aucune des propositions ci-dessus.
Le tableau suivant indique la valeur du champ de pesanteur g pour 6 planètes du système solaire :
| Planète | Mars | Mercure | Vénus | Saturne | Terre | Jupiter | | g (m s-2) | 3,7 | 3,8 | 8,6 | 9,1 | 9,8 | 22,9 |
Les vecteurs sont écrits en gras et en bleu.
On note v(t) = v k
la vitesse d'une bille métallique animée d'un mouvement de chute libre
verticale sur une de ces planètes. La représentation graphique de v(t)
est donnée ci-dessous. La bille atteint le sol sans rebondir.
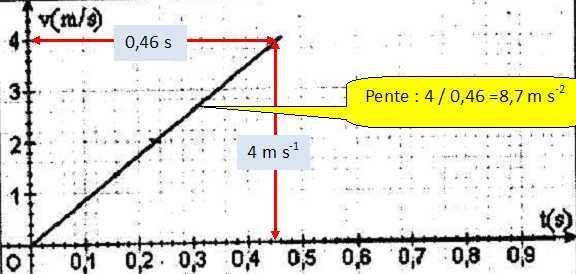
Quels sont les sens des vecteurs repérant le mouvement ?
A) le vecteur vitesse v(t) est ascendant. ( la vitesse croît, la chute est verticale vers le bas ).
B) le vecteur directeur k est ascendant.
C) Les vecteurs v et k sont de sens contraire. ( v est positif, v et k sont de même sens ).
D) le vecteur directeur k est descendant. Vrai.
E) Aucune des propositions ci-dessus.
Après avoir calculé l'accélération de la bille, dire sur quelle planète est la chute.
A) Terre ; B) Saturne ; C) Jupiter ; D ) Mars ; E) Aucune des propositions ci-dessus.
Le graphe donne 8,7 m s-2, ce qui correspond à Vénus.
Les lois de kepler dans le référentiel héliocentrique :
A ) les orbites des planètes sont des ellipses dont le centre S du soleil est l'un des foyers. Vrai.
B ) Pendant une durée Dt, l'aire balayée DA par le rayon joignant le centre du soleil au centre de la planète dépend de la position de la planète sur son éllipse.
Deuxième loi ou loi des aires : le mouvement de chaque planète est tel
que le segment de droite reliant le soleil et la planète balaie des aires égales
pendant des durées égales.
C) Lorsque la planète est au périhélie, sa vitesse orbitale est maximale. Vrai.
D
) Le carré de la période de révolution d'une planète est inversement
proportionnel au carré de la demi-longueur du grand axe de l'éllipse
décrite par cette planète.
Troisième loi de Kepler : pour toute les planètes, le rapport entre le cube du demi grand axe de la
trajectoire et le carré de la période est le même.
E) Aucune des propositions ci-dessus.
|
| .
. |
A ) La période de révolution de la terre est d'environ 24 h.
B) Dans le référentiel géocentrique, un satellite géostationnaire est en orbite dans le plan équatorial. Vrai.
C ) Dans le référentiel géocentrique, le centre de la terre est immobile. Vrai. ( C'est l'origine du repère ).
D ) le rayon de la trajectoire d'un satellite géostationnaire est environ 12 103 km. ( ~ 42 000 km ).
E) Aucune des propositions ci-dessus.
Le
8 février 1985, le lanceur Ariane III a mis en orbite géostationnaire,
supposée circulaire dans le référentiel géocentrique, le satellite
Arabsat F1.
Masse de la terre M = 6 1024 kg ; G = 6,67 10-11 m3 kg-1 s-2 ; rayon de la terre R =6400 km.
A ) La vitesse angulaire de ce satellite est w = 7,27 10-5 rad/s. Vrai.
Le satellite a la même vitesse angulaire que la terre w = 2 p / T = 2*3,14 / (24*3600) = 7,27 10-5 rad/s.
B ) La vitesse angulaire de ce satellite est w = 0,26 rad/s.
C ) L'altitude de ce satellite est h = 12 800 km.
D ) L'altitude de ce satellite est h ~ 35 900 km. Vrai.
(h+R)3 = GMT2 / (4p2) =6,67 10-11*6 1024 *(24*3600)2 / (4*3,142) =7,56 1022 ; R+ h = 4,23 107 m = 4,23 104 km ; h ~3,6 104 km.
E) Aucune des propositions ci-dessus.
Mouvement circulaire uniforme.
On
considère un satellite terrestre en mouvement circulaire uniforme dans
le référentiel géocentrique. On note r le rayon de la trajectoire, v sa
vitesse, w sa vitesse angulaire et T sa période orbitale.
A ) T = 2 p w. ( w = 2 p f = 2p / T ).
B ) T = 2 p r / v. Vrai. ( La circonférence 2 p r est parcourue à la vitesse v en une période T : 2 p r = v T ).
C ) v = w / r. ( v = w r )
D ) v = r w2.
E) Aucune des propositions ci-dessus.
|
|

