.
|
|
Un circuit
électrique comprend un condensateur de capacité C et une résistance R
montés en série. Après avoir déchargé le condensateur, on applique aux
bornes de l'ensemble RC une tension constante. On recueille aux bornes
du condensateur une tension variable représentée ci-dessous.
 
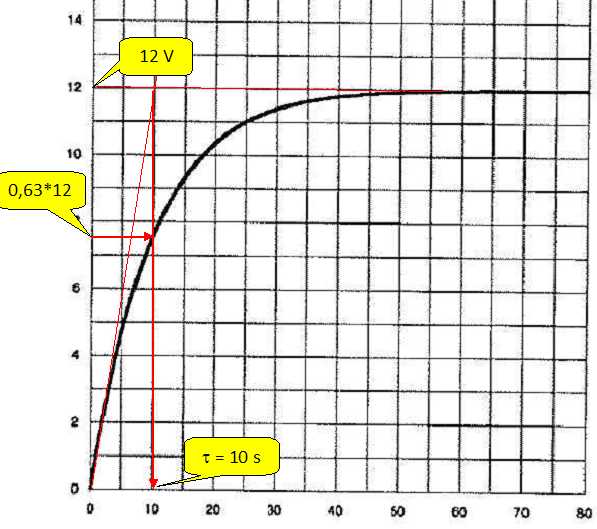
Quelle
tension ( en V ) est appliquée au bornes de RC ?
( 5 ; 12
; 14 ; 15 ; 120 ).
La tension aux bornes du
condensateur chargé est égale à la tension aux bornes du générateur.
Quelle
est en seconde la constante de temps de l'ensemble RC ? (3
; 5 ; 10
; 15 ; 20 )
Quelle est
en ohms la valeur de la résistance R ?
A) 20 ; B) 200 ; C) 200 000
C) On ne dispose pas d'assez de données pour calculer R. Vrai.
Il manque la
valeur de C.
E) On pourrait calculer R si on disposait de la courbe traduisant la
tension aux bornes de C pendant sa décharge à travers la résistance R.
Dipole
(RL).
On veut vérifier la valeur de la résistance r d'une bobine réelle
d'inductance L =0,250 H.
 |
| .
. |
Essai
1 : en régime permanent.
On réalise un circuit comportant un générateur de tension continue de
valeur E = 6,0 V de résistance interne négligeable, un ampèremètre
numérique, un voltmètre numérique, des fils de connection et la bobine
étudiée.
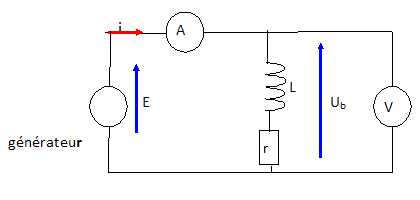
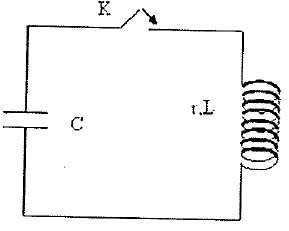
Compléter
le schéma du circuit en indiquant les positions de l'ampèremètre et du
voltmètre. Faire figurer la tension E aux bornes du générateur et Ub
aux bornes de la bobine. On négligera
la tension aux bornes de l'ampèremètre.
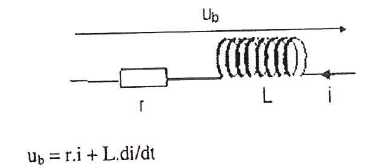
Ub = 5,95 V ; i = 410 mA. Calculer r
en justifiant.
En régime permanent, l'intensité est
constante ( di/dt=0) et la tension aux bornes de la bobine vaut Ub
= r i ; r = Ub/i = 5,95 / 0,410 =14,5 ohms.
Essai
2 : en régime transitoire.
On ajoute en
série une résistance R' = 10,0 ohms au circuit précédent. Il remplace
les appareils de mesure par un système d'acquistion informatisé qui lui
donne les variations de i(t) obtenues à la fermeture de l'interrupteur.
La tension du générateur reste fixe et égale à 6,00 V.
Quel est
le phénomène observé dans le circuit ?
On
observe un rerard à l'établissement du courant, retard pendant lequel
la bobine stocke de l'énergie.
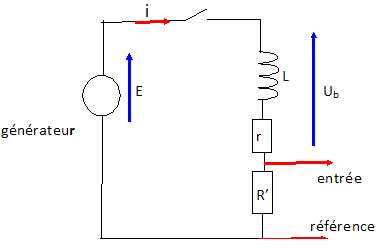
Sur le
circuit modifié indiquer comment brancher le système d'acquisition (
voie d'entrée et voie de référence) afin d'obtenir une tension
proportionnelle à l'intensité. Justifier.
La tenion aux bornes de la résistance R' est proportionnelle à
l'intensité i ; visualiser cette tension, c'est visualiser l'intensité
au facteur R' = 10 ohms près.
Déterminer
graphiquement la constante de temps en justifiant.
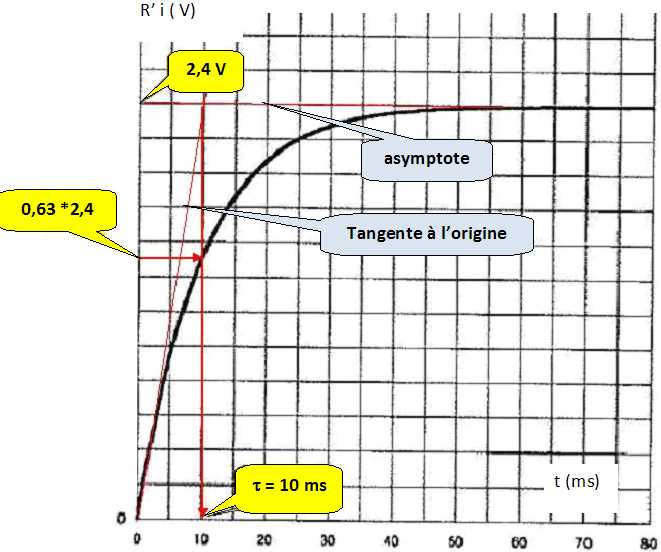
La valeur de t est égale à L/R
où R est la résistance totale du circuit.
Exprimer t en fonction des
paramètres du circuit et vérifier par analyse dimensionnelle que t est homogène à
un temps.
t
= L / (r+R') ;
Energie stockée par la bobine : ½Li2 ; L est une
énergie divisée par une intensité au carré ( J A-2).
Energie dissipée par effet Joule : Ri2t ; R est
une énergie divisée par une intensité au carré et par
un temps ( J
A-2s-1)
L/R a bien la dimension d'un temps.
Calculer
r.
r = L/t-R'
= 0,250 / 0,010 -10 =15 ohms.
On considère que l'intensité atteint sa valeur limite I = 240 mA au
bout d'une durée 5 fois supérieure à la constante de temps.
Quel est
le régime de fonctionnement de la bobine ?
Régime permanent.
Exprimer r
en fonction de E, I et R'. Calculer r.
E = (r+R') I ; r = E/I -R' = 6,00 / 0,240 -10 = 15 ohms.
Les trois valeurs de r sont cohérentes entre elles : écart relatif (
15-14,5) *100 / 15 =3,3 %.
Régime
oscillatoire.
La bobine est branchée aux bornes d'un condensateur de capacité C = 4
µF, préalablement chargé.
Rappeler
l'expression de la période propre d'un oscillateur LC. Calculer
cette période.
T0 = 2 p(LC)½=
2*3,14 (0,250 *4 10-6)½
~6,28 10-3 s = 6,28 ms.
On branche un oscilloscope aux bornes du condensateur et on observe sur
l'écran des oscillations pseudo-périodiques de pseudo-période T.
Interpréter
l'amortissement des oscillations.
Au cours des échanges d'énergie entre condensateur et bobine, une
partie de celle-ci est dissipée par effet Joule dans les parties
résistives du circuit.
On constate, avec une base de temps de 2 ms / div, que deux
pseudo-périodes occupent entre 6,2 et 6,4 divisions.
Donner
un encadrement de T et comparer T à T0.
6,2 *2 = 12,4 ms ; 6,4 *2 = 12,8 ms ; 12,4 < 2T
< 12,8 ms. 6,2 < T
< 6,4 ms.Valeur
T ~6,3 ms.
(T-T0) / T0 = (6,3 -6,28)
/ 6,28 *100= 0,3 %.
|
|






