Le
traitement du cancer thyroïdien comportetrès souvent deux temps : une
intervention chirurgicale qui enlève la glande thyroïde, puis
l'administration d'un radioélément sous forme d'iodure de sodium.
L'isotope utilisé est l'iode 131 noté 131I de période 8
jours. Lors de sa transformation radioactive spontanée, il émet une
particule béta moins et un photon gamma très énergétique. Cet iode
radioactif se fixe sur les reliquats de thyroïde laissés par le
chirurgien et les détruit.
|
|
Iode 131.
Pourquoi la
transformation radioactive de l'iode 131 entraîne-t-elle une émission
radioactive ß- ?
A) parce que son noyau contient trop de protons.
B) parce que son noyau contient trop de neutrons. Vrai.
C) parce que son noyau contient trop d'électrons
D) parce que son noyau contient trop de photon gamma
E) parce que son noyau est trop lourd.
13153I
---> 13154Xe + 0-1e
ou bien 10n--->11p + 0-1e
; un neutron se transforme en proton.
On veut administrer à une patiente déja opérée une activité d'iode 131
de 4 GBq. On dispose d'une gelule d'iodure de sodium d'activité 16 GBq.
Combien
de jours doit-on attendre pour l'administrer à la patiente ? (
2 ; 4 ; 8
; 16
; 32 )
A chaque période
l'activité initiale est divisée par deux ; au bout de 2 périodes
l'activité initiale est divisée par 4.
Quelle
est la constante radioactive ( en s-1) de l'iode 131 ?
( 10-2 ; 10-4 ; 10-6 ; 10-8
; 10-10 ).
l = ln2 / t½
= ln2 / (8*24*3600) ~1,0 10-6 s-1.
On a administré à la patiente 4
GBq d'iode 131.
Quel nombre d'atomes
d'iode représente cette activité ? 6 108
; 6 1010 ; 8 1012 ; 5 1014 ; 4 1015.
N = A / l = 4 109
/ 1,0 10-6 =4 1015.
Quelle
masse d'iode ( en µg) représente cette activité ? (0,34 ; 0,87 ; 1,89 ; 43,8 ; 521
)
Quantité de matière
d'iode 131 n = N / NA = 4 1015
/ 6 1023 =6,67 10-9
mol
m = n M(iode) = 6,67 10-9
*131 =8,7 10-7 g = 0,87 µg.
La plus grande partie de l'iode 131 est éliminé par les urines
lesquelles sont recueillies dans une cuve. L'une des cuves contient
51,2 GBq le lundi 7 mars 2011.
Quelle
sera l'activité ( en GBq ) présente dans cette cuve le lundi 2
mai 2011 ? ( 6,4 ; 0,512 ; 0,400 ; 0,200 ; 0,064 )
Entre le 7 mars et le 2
mai 2011 il y a : 56 jours soit 7 périodes.
L'activité initiale sera
donc divisée par 27 : 51,2 / 27
= 0,40 GBq.
|
| .
. |
Tomographie par
émission de positons.
|
La tomographie par émissions de positons : 4 points .
" Les neurobiologistes disposent d'une panoplie de
techniques d'imagerie dont chacune révèle des aspects particuliers de
l'architecture et du fonctionnement du cerveau. […] La tomographie par
émissions de positions, TEP, […] donne accès aux variations du flux
sanguin, lesquels reflètent l'activité métabolique cérébrale, […].
De cette découverte a germé l'idée que l'on […]
pourrait observer de l'extérieur l'activité siégeant à l'intérieur du
crâne.
En TEP, on détecte les molécules d'eau [présentes en
grande quantité dans le cerveau] en utilisant de l'eau radioactive que
l'on injecte au sujet par voie intraveineuse. […]. Dans ces molécules
d'eau radioactives, le noyau d'oxygène qui comprend normalement huit
protons et huit neutrons est remplacé par un noyau d'oxygène qui ne
comporte que huit protons et sept neutrons : c'est l'oxygène 15.
L'oxygène 15 est un émetteur b+
: un de ses protons se transforme rapidement en neutron, en émettant un
positon(1) et un neutrino(2). "
D'après un article de la revue Pour la Science, N° 302,
décembre 2002.
(1) Le positon est aussi appelé positron.
(2) Le neutrino est une particule de symbole
Données numériques :
|
Noyaux et particules
|
166C
|
157N
|
158O
|
155F
|
Électron
|
Positon
|
Neutron
|
Proton
|
|
Énergie de liaison par nucléon (MeV.nucléon-1)
|
6,676
|
7,699
|
7,463
|
6,483
|
|
|
|
|
|
Masse (kg)
|
|
|
|
|
9,0910 -31
|
9,109 10 -31
|
1,674 92 10 -27
|
1,672 62 10 -27
|
Célérité de la lumière dans le vide : c = 2,998 10 8 m.s-1
1 eV = 1,602 10 -19 J.
|
La désintégration de l'oxygène 15.
Donner,
en la justifiant, l'écriture symbolique X du noyau d'oxygène 15.
158O
: n°atomique ou nombre de charge Z=8.
nombre de
masse A=15 ; nombre de protons Z= 8 ; nombre de neutrons : 15-8=7.
Écrire
l'équation de la réaction de désintégration du noyau d'oxygène 15,
sans énoncer les lois de conservation et sans tenir compte de
l'émission du neutrino mentionné dans le texte. Le noyau fils n'est pas
produit dans un état excité.
158O --> 157N + 01e.
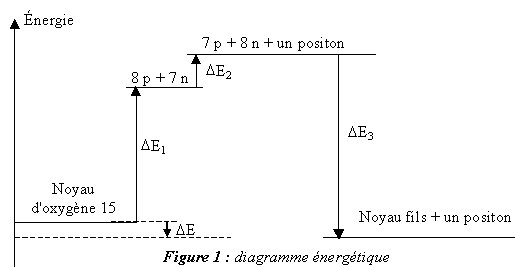
La variation d'énergie DE du système lors
de la désintégration d'un noyau d'oxygène 15 est indiquée sur la figure
1. Elle peut être calculée en utilisant le diagramme énergétique de
cette figure.
 Définir
l'énergie de liaison El du noyau.
Définir
l'énergie de liaison El du noyau.
On appelle énergie de liaison notée El d'un noyau l'énergie
que doit fournir le milieu extérieur pour séparer ce noyau au repos en
ses nucléons libres au repos.
On rappelle que l'énergie de liaison par nucléon est notée El/A
. Calculer, en
MeV, la variation d'énergie DE1 indiquée sur la
figure 1.
DE1 = Énergie de liaison
par nucléon * nombre de nucléons = 7,463*15 = 111,94 MeV.
En utilisant les masses des particules, calculer, en MeV,
la variation d'énergie DE2 indiquée sur la
figure 1 (on donnera le résultat final avec deux chiffres
significatifs).
DE2 : un proton se
transforme en neutron + émission d'un positon
DE2 =( masse neutron +
masse positon- masse proton )c²
DE2 = ( 1,674 92 + 9,109 10
-4 - 1,672 62 )10 -27 * (2,998
108)² = 2,89 10-13 J
2,89 10-13 / 1,6 10-19 = 1,8 106 eV = 1,8 MeV.
Déduire
des résultats précédents la valeur, exprimée en MeV, de la variation
d'énergie D E du système lors de
la désintégration d'un noyau d'oxygène 15.
D E = DE3
+DE1 + DE2 ;
DE3 =
- El(157N )=-7,699*15 = -115,5 MeV. D E
= -115,5+111,9+1,8 = -1,8 MeV.
L'utilisation de l'oxygène 15 en
TEP.
" Le positon est l'antiparticule de
l'électron, […]. Matière et antimatière s'annihilent(3) dès qu'elles
sont en présence : un positon et un électron du milieu environnant
s'annihilent en libérant une paire de photons d'énergie déterminée (511
kiloélectronvolts). Les deux photons sont émis dans deux directions
diamétralement opposées. […]
L'objet de la TEP est de repérer les photons […], très énergétiques,
[qui] traversent en grande partie le cerveau et le crâne, de sorte que
l'on peut les détecter en dehors de la boite crânienne. Le dispositif
de détection, la caméra à positons, […] entoure la tête du sujet. […]
Lorsqu'une paire de photons gamma de 511 kiloélectronvolts arrive
simultanément sur deux détecteurs […], on admet qu'ils sont issus de la
dématérialisation d'un même positon (figure 2). […]. Après l'analyse
mathématique, on obtient une série de " coupes " contiguës du cerveau
qui représentent la concentration en noyaux d'oxygène 15 en chaque
point ce qui reflète le débit sanguin local.
Enfin, le temps de demi-vie de ces noyaux d'oxygène 15 émetteurs de
positons est bref : 123 secondes. Cette propriété est importante dans
le contexte de l'utilisation de ces molécules chez l'homme, car, d'une
part l'irradiation subie par les sujets est faible et d'autre part
cette radioactivité disparaissant rapidement, on peut faire plusieurs
études chez le même sujet. Cette courte durée de vie impose néanmoins
que l'eau radioactive soit préparée dans les minutes qui précèdent son
injection, et que deux injections successives soient espacées de 8 à 10
minutes. "
(3) Annihiler : réduire
à rien ; détruire, anéantir. En physique, transformation intégrale de
l'énergie de masse en énergie transportée par une onde
électromagnétique.
Définir le temps de
demi-vie t1/2 .
Le temps de demi-vie t½ ou période est la durée au bout de
laquelle la moitié des noyaux initialement présents se sont désintégrés.
L'évolution
temporelle du nombre de noyaux d'oxygène 15 est donnée par la loi de
décroissance où N0 est le nombre de noyaux d'oxygène 15 au
moment de l'injection à l'instant de date t = 0 s.
À
partir de cette loi, montrer que la constante radioactive l a pour expression :
l = ln 2 / t1/2 . Calculer sa valeur.
Loi de
écroissance radioactive : N
= N0 exp(-lt) ou ln( N0 /N)= lt.
pour t = t½ , N= ½N0
soit N0 /N =2: ln 2 = l t½.
l = ln2 / t½ = ln2 / 123 = 5,64 10-3
s-1.
Si l'on souhaite
poursuivre l'examen par TEP, on estime qu'il est nécessaire de procéder
à une nouvelle injection dans l'organisme du patient lorsque le nombre
N(t1) de noyaux d'oxygène 15 restant à
l'instant de date t1 est de l'ordre de 5% du nombre N0
de noyaux initialement injectés. Calculer la valeur
de la date t1.
- Justifier la
durée d'espacement des injections évoquée dans le texte.
Pour t= t1, N= 0,05 N0
soit N0 /N = 20. ln( 20)= 5,64 10-3
t1 soit t1
= 531 s. (environ 9 minutes). D'où la durée
entre deux injections successives.
La
détection du rayonnement gamma.
En utilisant le
texte, écrire l'équation de la réaction ayant lieu lors de la rencontre
d'un positon, issu de la désintégration d'un noyau d'oxygène 15, avec
un électron du milieu environnant. On
notera g chaque photon gamma émis.
01e
+ 0-1
e --> 2 photons g.
On admet que l'énergie
libérée par cette réaction est partagée également entre les deux
photons dont la masse est nulle.
Calculer l'énergie de
chaque photon gamma émis. Est-elle en accord avec celle donnée dans le
texte (aucun calcul d'écart relatif n'est demandé.
Annihiler :
transformation intégrale de l'énergie de masse en énergie transportée
par une onde électromagnétique.
soit 2* 9,109 10 -31 *(3 108)²
= 1,64 10-13 J.
1,64 10-13 / 1,6 10-19 = 1,024 106
eV pour deux photons.
énergie d'un photon g : 5,12 105
eV = 512 keV ( en accord avec le texte).
|
|
